Линейные неоднородные уравнения с постоянными коэффициентами

Лекция 12

При решении линейных неоднородных уравнений с постоянными коэффициентами во многих случаях без труда удается подобрать частные решения и тем самым свести задачу к интегрированию соответствующего однородного уравнения.

Пусть, например, правая часть является полиномом степени 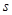, и, следовательно, уравнение имеет вид

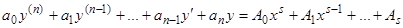, (1)

где все и — постоянные.

Если , то существует частное решение уравнения (1), также имеющее вид полинома степени 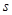. Действительно, подставляя 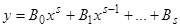в уравнение (1) и сравнивая коэффициенты при одинаковых степенях 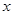в левой и правой частях, получаем для определения коэффициентов 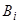всегда разрешимую, если , систему линейных уравнений:

,

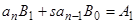, откуда определяется ,

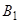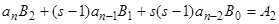, откуда определяется ,

……………………………………………………………………

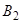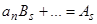, откуда определяется .

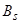Итак, если , то существует частное решение, имеющее вид полинома, степень которого равна степени полинома, стоящего в правой части.

Предположим теперь, что 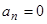, причем для общности допустим, что и 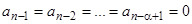, но 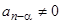, т.е. является -кратным корнем характеристического уравнения, причем случай 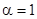не исключается. При этом уравнение (1) принимает вид

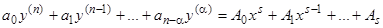. (2)

Полагая 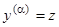, мы приходим к предыдущему случаю, и следовательно, существует частное решение уравнения (2), для которого 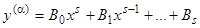, а значит, 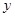является полиномом степени , причем слагаемые, начиная со степени 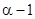и ниже, у этого полинома будут иметь произвольные постоянные коэффициенты, которые, в частности, могут быть выбраны равными нулю. Тогда частное решение примет следующий вид: .

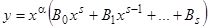Пример 1. 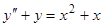. Частное решение имеет вид . Подставляя в исходное уравнение и сравнивая коэффициенты при одинаковых степенях 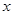, получаем . Общее решение .

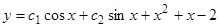Пример 2. 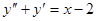. Частное решение ищем в виде 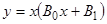. Подставляя в уравнение и сравнивая коэффициенты при одинаковых степенях 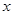в левой и правой частях полученного тождества, находим , 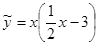. Общее решение .

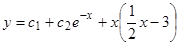Рассмотрим теперь линейное неоднородное уравнение вида

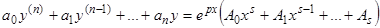, (3)

где все 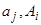— постоянные. Как мы рассматривали ранее, замена переменных 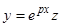преобразует уравнение (3) к виду

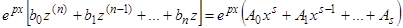, или

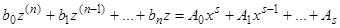, (4)

где все 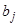— постоянные.

Частное решение уравнения (4), если 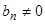, имеет вид 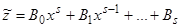, а значит, частное решение уравнения (3) 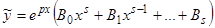. Условие 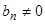означает, что 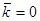не является корнем характеристического уравнения

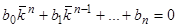, (5)

а следовательно, 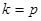не является корнем характеристического уравнения

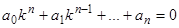, (6)

так как корни этих характеристических уравнений так же, как и раньше, связаны зависимостью .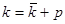

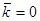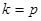Если же является корнем характеристического уравнения (5) кратности , другими словами, является корнем характеристического уравнения (6) той же кратности , то частные решения уравнения (4) и (3) имеют соответственно вид , .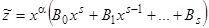

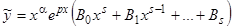Итак, если правая часть линейного дифференциального уравнения с постоянными коэффициентами имеет вид 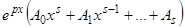, то, если 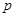не является корнем характеристического уравнения, частное решение надо искать в таком виде: 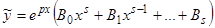. Если же 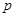является корнем характеристического уравнения кратности (этот случай называется особым или резонансным), то частное решение надо искать в виде .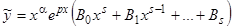

Пример 3. 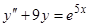. Частное решение надо искать в виде .

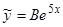Пример 4. 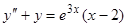. Частное решение надо искать в виде .

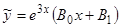Пример 5. 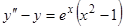. Частное решение надо искать в виде , так как является простым корнем характеристического уравнения.

Пример 6. 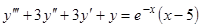. Частное решение надо искать в виде 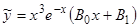, так как 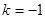является трехкратным корнем характеристического уравнения.

Заметим, что наши рассуждения остаются справедливыми и при комплексном 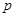, поэтому если правая часть линейного дифференциального уравнения имеет вид

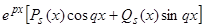, (7)

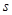где один из полиномов или имеет степень , а другой — степень не выше чем 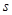, то, преобразуя тригонометрические функции по формулам Эйлера к показательному виду, получим в правой части

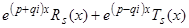, (8)

где 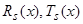— полиномы степени .

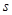Для каждого слагаемого правой части можно уже применить записанное нами правило, а именно, если 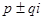не являются корнями характеристического уравнения, то частное решение можно искать в таком же виде, как и правая часть (8). Если же 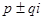являются корнями характеристического уравнения кратности , то частное решение приобретает множитель .

Если опять вернуться к тригонометрическим функциям, то это правило можно сформулировать так:

а) Если 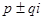не являются корнями характеристического уравнения, то частное решение надо искать в ви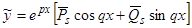де , где 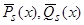— полиномы степени 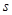с неопределенными коэффициентами.

Заметим, что если один из полиномов 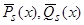имеет степень ниже 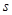или даже, в частности, тождественно равен нулю, то все же оба полинома 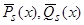будут, вообще говоря, иметь степень .

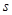б) Если 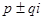являются -кратными корнями характеристического уравнения (резонансный случай), то частное решение надо искать в виде .

Пример 7. 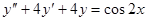. Так как числа не являются корнями характеристического уравнения, то частное решение ищем в виде .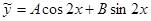

Пример 8. . Так как числа являются простыми корнями характеристического уравнения, то частное решение ищем в виде .

Пример 9. 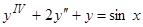. Так как числа 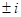являются двукратными корнями характеристического уравнения, то частное решение ищем в виде .

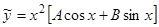Пример 10. 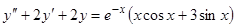. Так как числа 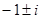являются простыми корнями характеристического уравнения, то частное решение ищем в виде .

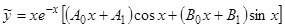Во многих случаях при нахождении частных решений линейных уравнений с постоянными коэффициентами с правой частью вида (7) целесообразно перейти к показательным функциям.

Например, в уравнении 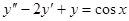можно преобразовать 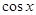по формуле Эйлера или, еще проще, рассмотреть уравнение 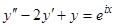, действительная часть решения которого должна удовлетворять исходному уравнению согласно доказанной нами теореме. Частное решение этого уравнения можно искать в виде 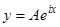. Тогда . Частное решение исходного уравнения .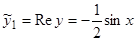

Для нахождения частных решений линейных неоднородных уравнений с постоянными коэффициентами во многих случаях очень удобен операторный метод.