2015-02-18
828
Пример 1. Статическое нагружение прямоугольной шарнирно-опертой пластинки.
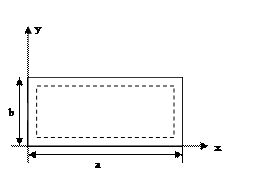Уравнение состояния в декартовых координатах будет иметь следующий вид:
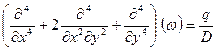
Решение задачи удобно представить в виде двойного тригонометрического ряда:
(*)
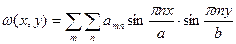Правая часть представляет разложение в аналогичный ряд:
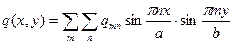
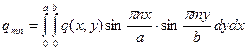
Дифференцируя уравнение (*) надлежащее количество раз, получим
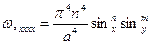
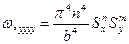
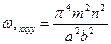
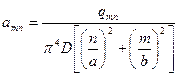
Нетрудно убедиться, что приведенное решение удовлетворяет краевым условиям и дифференциальному уравнению состояния.
Пример 2. Шарнирно-опертая по контуру прямоугольная пластинка, нагруженная сосредоточенной силой, статически приложенной в точке с координатами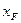 
, 
.
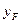Наиболее просто задачи со сосредоточенными силами и моментами решаются методом Ритца-Галеркина с использованием вариационного уравнения с изгибом.
Уравнение (*) рассматривается как разложение прогиба по функциональному базису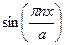 
, 
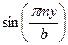, коэффициенты которого следует определять из вариационного уравнения. При вычислении этих коэффициентов следует учесть, что
|
|
|
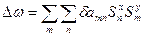
Входящие в вариационное уравнение произведения кривизны выражаются через базисные тригонометрические функции и могут быть легко вычислены с учетом свойств тригонометрических функций.
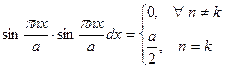
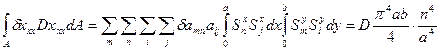
Преобразуя аналогично остальные составляющие вариационного уравнения, запишем выражение элементарной работы внутренних сил:
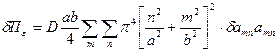
В уравнении (2.140) отсутствует распределенная нагрузка, но имеется сосредоточенная сила, которая производит работу на перемещение представленной функции (*).
Дополним уравнение (2.140) элементарной работы сосредоточенной силой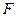 
.
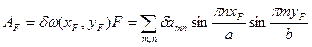
Т.к. вариация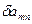 
есть независимая, одновременно 
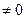числа, то для определения 
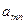имеем систему уравнений с диагональной матрицей:
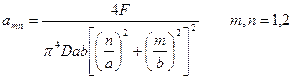
Пример 3. Свободные колебания прямоугольной шарнирно-опертой пластинки.
В уравнении (2.140) учтем силы инерции. Элементарная работа этих сил будет следующей:
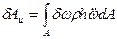
Или с учетом разложения (*), приводится к виду:
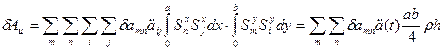
Учитывая, что 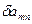- независимая, 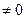функция, получаем обыкновенную дифференциальную систему второго порядка для определения коэффициентов .
,
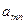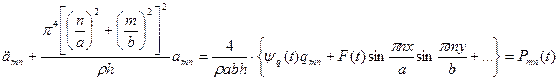где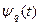 
- закон изменения распределенной нагрузки по времени.
Считается, что сосредоточенная сила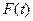 
изменяется по заданному закону. Для сокращения обозначается 
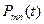. Если ввести обозначение
,
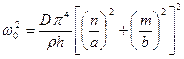то система дифференциальных уравнений для пластинки приобретает вид модального разложения:
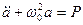
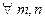
Зависимость коэффициентов (*) от времени определяется интегралом Дюамеля:
(**)
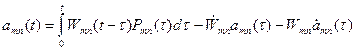Импульсно-переходная переменная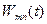 
есть:
.
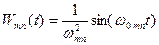При решении задачи о свободных колебаниях в формуле (**)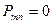 
и закон движения произвольной точки пластинки описывается уравнением:
|
|
|
.
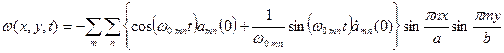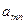и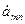 
находятся из разложения начальных условий в двойной тригонометрический ряд:
,
.
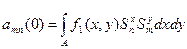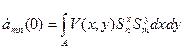Пример 4. Вынужденные колебания прямоугольной шарнирно-опертой пластинки.
Решение задачи определяется (**) при однородных начальных условиях:
,
.
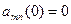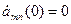Решение конкретной задачи сводится к вычислению интеграла по времени вида:
.
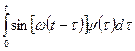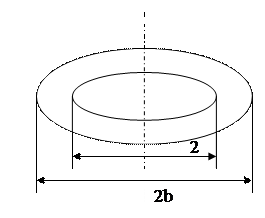Пример 5. Пластинка в виде кругового кольца, нагруженная симметрично относительно оси.
Перейдем к полярным координатам в уравнении Софии Жорне:
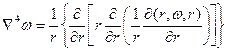
Уравнение Софии Жорне является обыкновенным дифференциальным уравнением при статическом нагружении и гиперболическим уравнением с двумя переменными при динамическом нагружении.
Задача статики: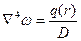 
решается четырехкратным интегрированием.
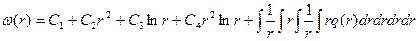
Для такого состояния пластинки можно давать перемещение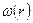 
, угол поворота 
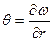, радиальный изгибающий момент 
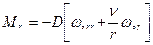и перерезывающую силу 
.
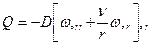Для сплошной пластинки (без центрального отверстия) следует поставить условие ограниченности прогиба в центре, положив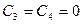 
.
При решении динамических задач для круглых пластинок уравнение состояния имеет вид:
,
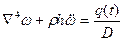решение которого (форма свободных колебаний) представляется через функции Бесселя I и II рода.
,
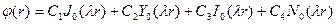где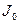 
- функция Бесселя 0 порядка I рода;
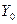- функция Бесселя 0 порядка II рода;
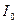- модифицированная функция Бесселя 0 порядка I рода;
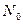- модифицированная функция Бесселя 0 порядка II рода;
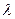- определяет частоты свободных колебаний, находящиеся из характеристического уравнения, выражающего равенство нулю определителя системы линейных алгебраических уравнений относительно 
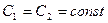, реализующий краевые условия.
Характеристическое уравнение трансцендентное и его решение следует искать численными методами.
Форма свободных колебаний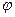 
определяется как собственные векторы характеристической системы уравнений, и также обладают свойством ортогональности.
Располагая выражением для собственных форм колебаний, определяют спектр собственных частот по формуле
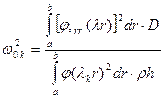
Поперечное перемещение (прогиб) пластинки представляется разложением по собственным формам:
Коэффициенты разложения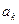 
определяются из системы обыкновенных дифференциальных уравнений такого же вида, что и в стержнях, и в прямоугольных пластинках.
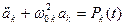
Правая часть определяется разложением распределенной нагрузки по формам свободных колебаний
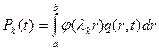
Начальные условия для коэффициентов 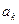определяются разложением по тому же базису начального прогиба и начальной скорости
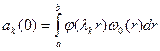
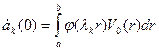
Коэффициенты разложения как и в предыдущих случаях определяются интегралом Бернулли:
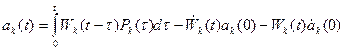
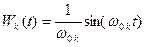
Как и ранее первое слагаемое описывает вынужденные колебания, а два последних – свободные.
