Справочный материал
Тригонометрическим называется уравнение, содержащее неизвестное под знаком тригонометрических функций.
Среди простейших тригонометрических уравнений рассмотрим следующие: 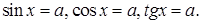
1) Уравнение
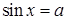 (5.1)
(5.1)
имеет решение, если 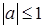 или
или 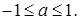
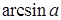 – это угол (дуга), синус которого равен a, расположенный либо в первой, либо в четвертой четверти:
– это угол (дуга), синус которого равен a, расположенный либо в первой, либо в четвертой четверти:
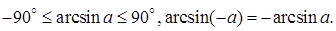
Общее решение уравнения (5.1) ищут в виде
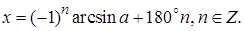 (5.2)
(5.2)
Частные случаи:
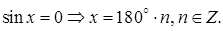 (5.3)
(5.3)
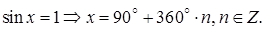 (5.4)
(5.4)
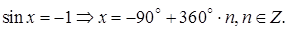 (5.5)
(5.5)
2) Уравнение
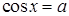
 (5.6)
(5.6)
имеет решение при условии, что 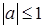 или
или 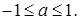
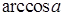 – это угол (дуга), косинус которого равен a, расположенный либо в первой, либо во второй четверти:
– это угол (дуга), косинус которого равен a, расположенный либо в первой, либо во второй четверти:
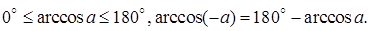
Общее решение уравнения (5.6) ищут в виде
 (5.7)
(5.7)
Частные случаи:
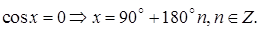 (5.8)
(5.8)
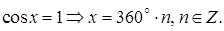 (5.9)
(5.9)
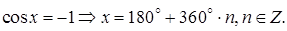 (5.10)
(5.10)
3) Уравнение
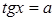 (5.11)
(5.11)
имеет решение при любом 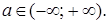
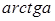 – это угол (дуга), тангенс которого равен a, расположенный либо в первой, либо в четвертой четверти:
– это угол (дуга), тангенс которого равен a, расположенный либо в первой, либо в четвертой четверти:
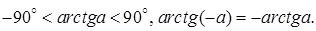
Общее решение уравнения (5.11) ищут в виде
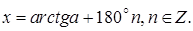 (5.12)
(5.12)
Используя тригонометрические формулы, любое тригонометрическое уравнение привести к одному из простейших видов (5.1) или (5.6), или (5.11).
Решить тригонометрическое уравнение, значит найти его общее решение.
 2015-02-18
2015-02-18 455
455








