5.1 Решить уравнение 
Решение. Применим формулу (5.2) и найдем общее решение исходного уравнения 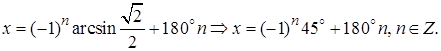
Ответ: 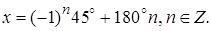
5.2 Решить уравнение 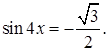
Решение. На основании формулы (5.2)
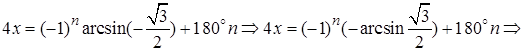
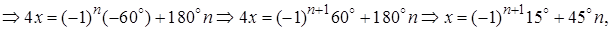
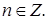
Ответ: 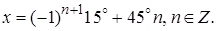
5.3 Решить уравнение 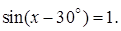
Решение. Согласно формуле (5.4) находим общее решение
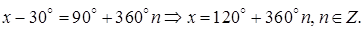
Ответ: 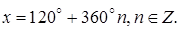
5.4 Решить уравнение 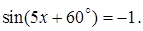
Решение. В соответствии с (5.5) находим общее решение
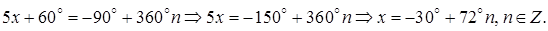
Ответ: 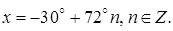
5.5 Решить уравнение 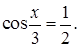
Решение. На основании формулы (5.7)
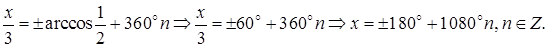
Ответ: 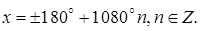
5.6 Решить уравнение 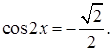
Решение. 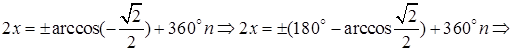
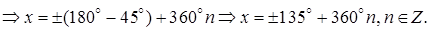
Ответ: 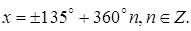
5.7 Решить уравнение 
Решение. В соответствии с (5.9) находим общее решение
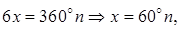
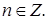
Ответ: 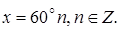
5.8 Решить уравнение 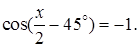
Решение. В соответствии с (5.10) общее решение имеет вид
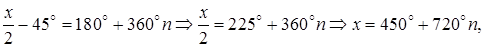
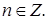
Ответ: 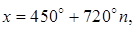
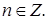
4.9 Решить уравнение 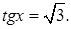
Решение. Применим формулу (5.12) и найдем общее решение
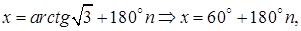
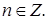
Ответ: 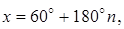
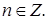
5.10 Решить уравнение 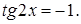
Решение. Общее решение
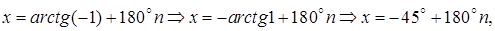
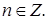
Ответ: 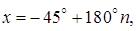
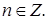
5.11 Решить уравнение 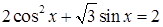 и найти
и найти 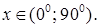
Решение. Применяя формулу 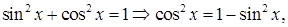 исходное уравнение приведем к виду
исходное уравнение приведем к виду
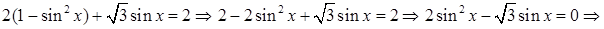
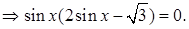
Возможны два случая:
1) 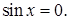 На основании (5.3) находим
На основании (5.3) находим 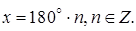
2) 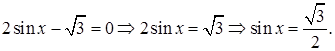 Применяя формулу (5.2), по-
Применяя формулу (5.2), по-
лучаем общее решение
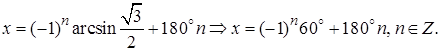 Полагая здесь
Полагая здесь 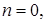 находим
находим 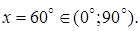
Ответ: 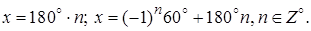
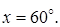
|
|
|
5.12 Решить уравнение 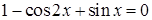 и найти
и найти 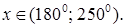
Решение. Используя формулу 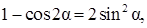 исходное уравнение приведем к виду
исходное уравнение приведем к виду 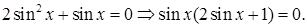
1) 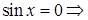
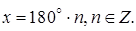
2) 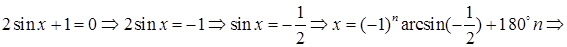
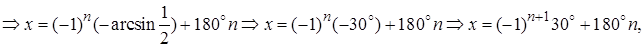
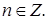 Полагая
Полагая 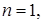 найдем
найдем 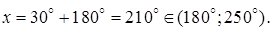
Ответ: 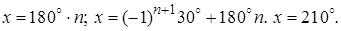
5.13 Решить уравнение 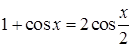 и найти
и найти 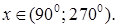
Решение. В соответствии с известной формулой 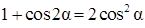 исходное уравнение приведем к виду
исходное уравнение приведем к виду
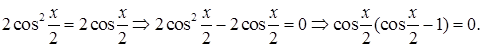
1) 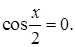 Согласно формуле (5.8)
Согласно формуле (5.8)
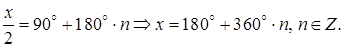 Полагая
Полагая 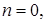 находим
находим
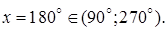
2) 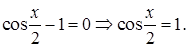 Тогда на основании (5.9)
Тогда на основании (5.9)
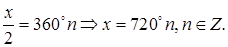
Ответ: 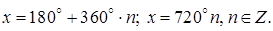
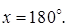
5.14 Решить уравнение 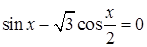 и найти
и найти 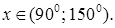
Решение. Применим формулу 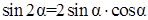 и получим уравнение
и получим уравнение
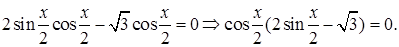
1) 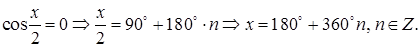
2) 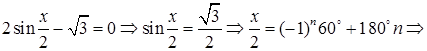
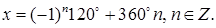 Если положить
Если положить 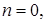 то найдем
то найдем
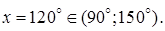
Ответ: 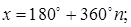
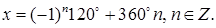
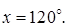
5.15 Решить уравнение 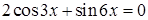 и найти
и найти 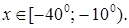
Решение.
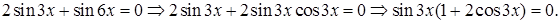
1) 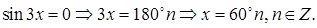
2) 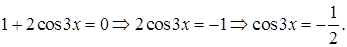 Общее решение найдем, применив (5.7):
Общее решение найдем, применив (5.7):
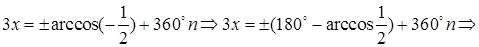
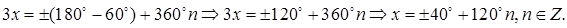
В последнем общем решении полагаем 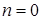 и выбираем знак «–». Находим
и выбираем знак «–». Находим 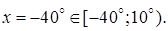
Ответ: 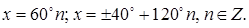
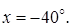
5.16 Решить уравнение 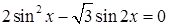 и найти
и найти 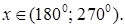
Решение. Преобразуем заданное уравнение
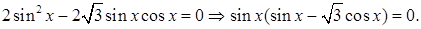
1) 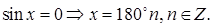
2) 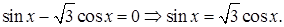 Разделим обе части последнего уравнения и получим
Разделим обе части последнего уравнения и получим 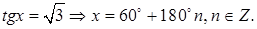 Если
Если 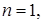 то
то
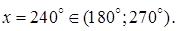
Ответ: 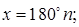
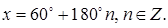
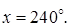
5.17 Решить уравнение  и найти
и найти 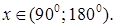
Решение. Так как 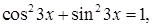 то исходное уравнение примет вид
то исходное уравнение примет вид
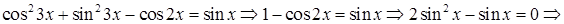
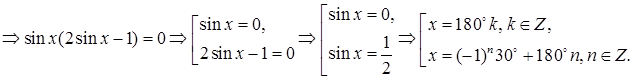
При 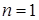 получаем
получаем 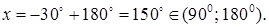
Ответ: 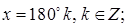
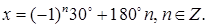
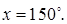
5.18 Решить уравнение 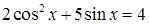 и найти
и найти 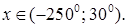
Решение. Из тригонометрического тождества 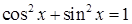 выразим
выразим 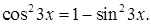 Тогдазаданное уравнение примет вид
Тогдазаданное уравнение примет вид
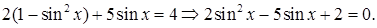
Введем новую переменную t так, что 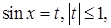 получим квадратное уравнение
получим квадратное уравнение 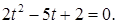 Находим дискриминант и корни:
Находим дискриминант и корни:
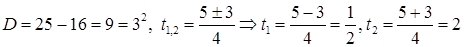 не удовлетворяет условию
не удовлетворяет условию 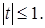 Далее,
Далее,
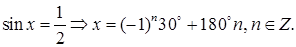
Если возьмем 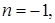 то найдем
то найдем 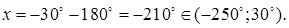
Ответ: 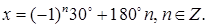
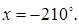
5.19 Решить уравнение 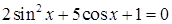 и найти
и найти 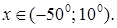
Решение. 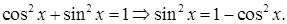 Тогдаполучим уравнение
Тогдаполучим уравнение
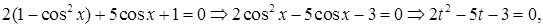 где
где 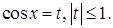
Находим 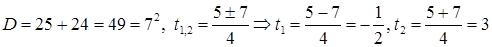 не удовлетворяет условию
не удовлетворяет условию 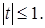 Следовательно,
Следовательно,
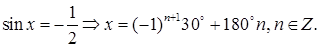
Положим 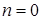 и найдем
и найдем 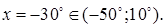
Ответ: 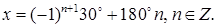
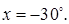
 2015-02-18
2015-02-18 698
698








