Примеры с решениями. Решение. Согласно определения логарифма

4.1 Решить уравнение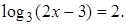

Решение. Согласно определения логарифма

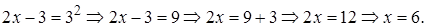
Проверка.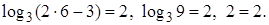

Ответ: 6.

Замечания: 1) Уравнения 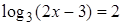и 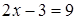равносильны, поэтому проверка необязательна. Если при выполнении задания вы затрудняетесь определить равносильность уравнений, делайте проверку или находите область допустимых значений. В одном задании делать проверку и находить область допустимых значений нет необходимости.

2) В дальнейшем в процессе решения каждого уравнения будем делать проверку, но в замечании к решению – находить область допустимых значений с целью научить вас этой процедуре.

Так как выражение под знаком логарифма должно быть положительным, то область допустимых значений уравнения 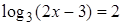находим из условия

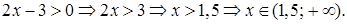Значение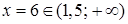

4.2 Решить уравнение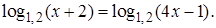

Решение. От исходного перейдем к уравнению

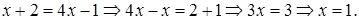
Проверка.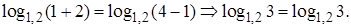

Ответ: 1.

Замечание. ОДЗ: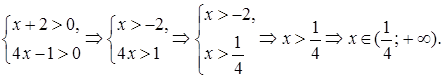

Значение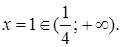

4.3 Решить уравнение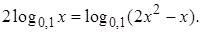

Решение. На основании свойств логарифмов уравнение принимает вид

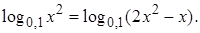
Тогда

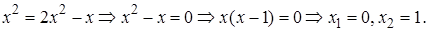
Проверка. 1) 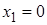– не корень, так как 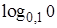не существует.

2)

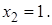
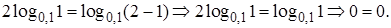
Ответ: 1.

Замечание. В заданном уравнении проще сделать проверку, чем находить ОДЗ, решая систему неравенств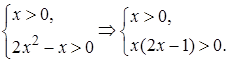

Для проверки правильности решения найденные значения неизвестного можно подставлять не в заданное уравнение, а в ОДЗ.

1) Значение 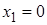системе неравенств 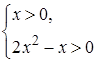не удовлетворяет,

поэтому 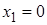– не корень исходного уравнения.

2) При 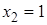система неравенств 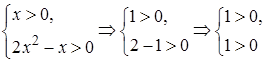выполняется, следовательно, 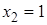– корень уравнения.

4.4 Решить уравнение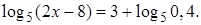

Решение. Так как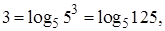

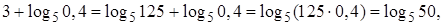
То заданное уравнение принимает вид

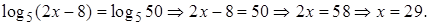
Проверка.

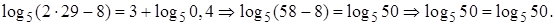
Ответ: 29.

Замечание. ОДЗ: 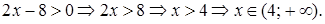Значение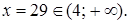

4.5 Решить уравнение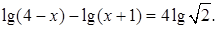

Решение. Используя свойства логарифмов, получаем уравнение

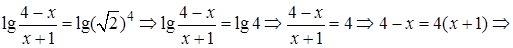
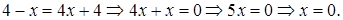
Проверка. 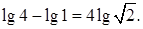Учитывая, что 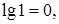находим, что

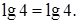
Ответ: 0.

Замечание. ОДЗ:

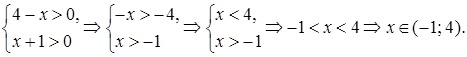Корень уравнения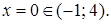

4.6 Вычислить 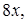где x – решение уравнения

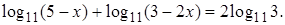
Решение. Применим свойства логарифмов и получим уравнение

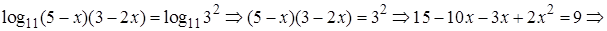
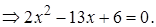Учитывая, что дискриминант 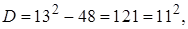находим корни квадратного уравнения

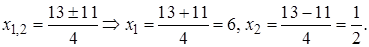
Проверка. 1) 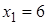– не корень, так как 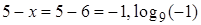не существует.

2)

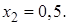
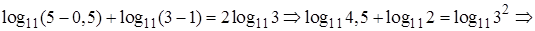
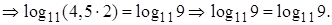
Вычислим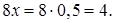

Ответ: 4.

Замечание. ОДЗ:

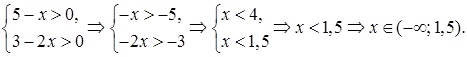
Значение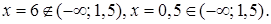

4.7 Решить уравнение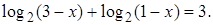

Решение. Применим свойства логарифмов и получим уравнение

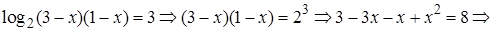
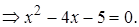Находим корни квадратного уравнения, используя теорему Виета: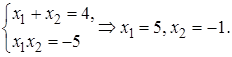

Проверка. 1) 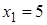– не корень, так как 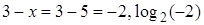не существует.

2)

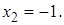
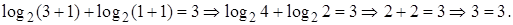
Ответ: -1.

Замечание. ОДЗ:

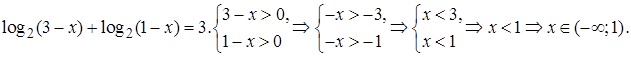
Значение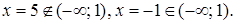

4.8 Решить уравнение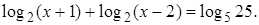

Решение. Поскольку 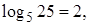то уравнение принимает вид

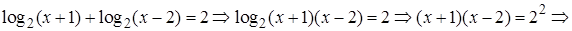
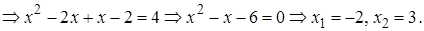
Проверка. 1) 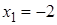– не корень, так как 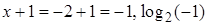не существует.

2)

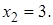
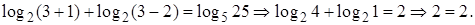
Ответ: 3.

Замечание. ОДЗ: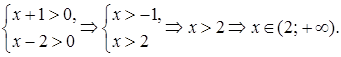

Значение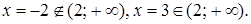

4.9 Решить уравнение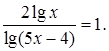

Решение.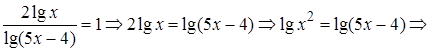

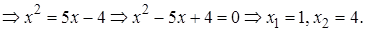
Проверка. 1) 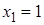– не корень, так как 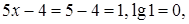делить на нуль нельзя..

2)

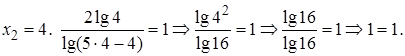
Ответ: 4.

Замечание. ОДЗ: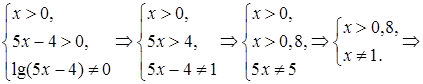

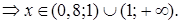
Значение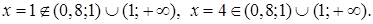

4.10 Решить уравнение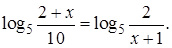

Решение. Исходя из условия получаем

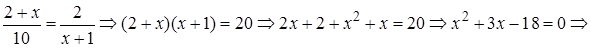
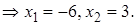
Проверка. 1) 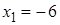– не корень, так как 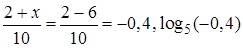не существует.

2)

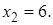
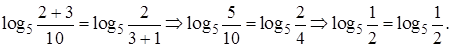
Ответ: 3.

Замечание. ОДЗ: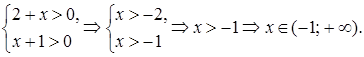

Значение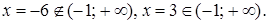

4.11 Решить уравнение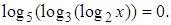

Решение.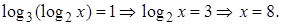

Проверка.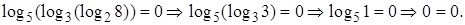

Ответ: 8.