Содержание лекции. Рассмотрим получение гармонической передаточной функции (Г-ПФ) идеального реле

Рассмотрим получение гармонической передаточной функции (Г-ПФ) идеального реле. Выходной сигнал будет иметь вид, показанный на рис. 2.26.

После аппроксимации выходного сигнала первым членом ряда Фурье в виде амплитуды выходного сигнала (на рис.2.26 показано штриховой жирной линией), получаем пределы измерения четверти выходной синусоиды от ωt = 0 до ωt = π /2. Эта часть синусоиды заштрихована. Вся амплитуда выходного сигнала определяется

Рис.2.26. Выходной сигнал идеального реле и его первая гармоника

Тогда Г- ФП идеального реле при выходном сигнале В и при амплитуде входного сигнала А

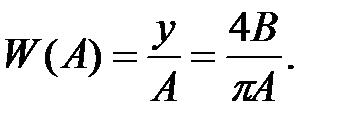
Таким образом, ограничиваясь рассмотрением первой гармоники на выходе нелинейного элемента при гармоническом сигнале на его входе, заданный вид нелинейности заменяют линейным уравнением, которое зависит от амплитуды входного сигнала А. Такая замена называется гармонической линеаризацией нелинейных зависимостей.

Рассмотрим, какие особенности имеет гармоническая передаточная функция при неоднозначной характеристике релейного элемента на примере такого элемента с гистерезисной характеристикой. Определение гармонической передаточной функции (Г-ПФ) нелинейного элемента будем производить при тех же двух условиях (смотри рисунок 2.21):

- на вход НЭ поступает сигнал x(t)= A·sinωt;

- ЛЧ системы обладает свойством фильтра.

Полученное значение выходного сигнала y(t) так же разложим в ряд Фурье и расчет проведём по основной гармонике y(t)=B₁sinωt + С₁cosωt, где B₁ – выходная величина реле, C₁ – характеризует влияние гистерезиса.

Коэффициенты ряда Фурье определяются по формулам

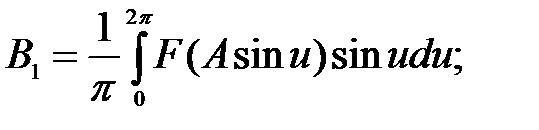
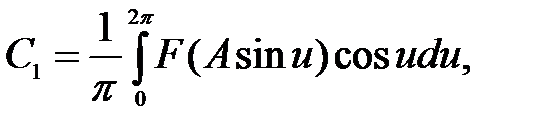
где u – переменная интегрирования, u = ωt.

Учитывая, что x(t) = Asinωt, тогда

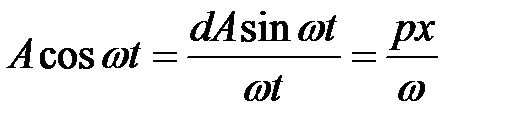
Обозначим отношение выходного сигнала к входному, который задан в виде амплитуды A через q(A) и q^’(A)

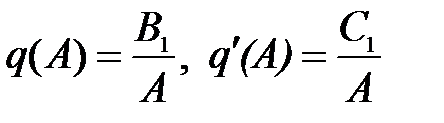
С учетом этих обозначений

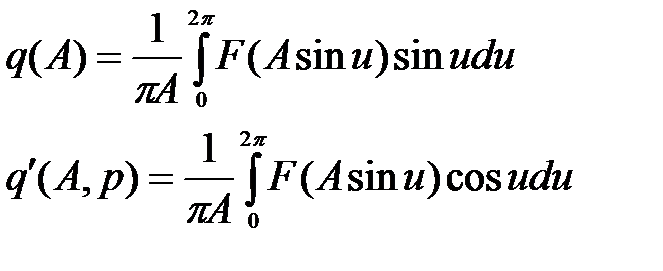
Тогда гармоническая передаточная функция

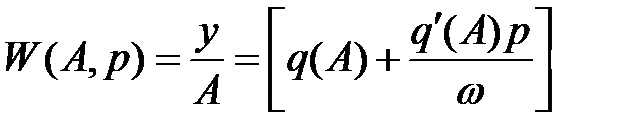
Для определения гармонической частотной передаточной функции сделаем подстановку p = jω

W(A,ω) = [q(A) + jq^’(A)]

Коэффициенты q(A) и q^’(A) называются коэффициентами гармонической линеаризации.

С помощью представления нелинейного элемента в виде гармонической передаточной функции достаточно просто на основании критерия Найквиста можно определить частоту и амплитуду автоколебаний. Этот способ известен в литературе как метод Гольдфарба. Для его использования необходимо предварительно преобразовать схему нелинейной системы так, чтобы все линейные элементы объединились в одну частотную передаточную функцию W_лч(jω). При этом нелинейный элемент представляют в виде гармонической частотной передаточной функции W_нэ(A) на входе системы. Тогда общая передаточная функция системы в разомкнутом состоянии W_раз(jω,A) = W_нэ(A)W_лч(jω).

Предположим, что замкнутая нелинейная система находится на границе устойчивости и в ней возникли незатухающие колебания (автоколебания). Тогда согласно критерию Найквиста амплитудно-фазовая характеристика разомкнутой системы Wраз(j ω,A) должна проходить через точку с координатами (-1, j0). Отсюда условие существования автоколебаний в замкнутой системе:

Wн.э(A)·Wл.ч(jω)· = -1.

Непосредственно построить эту амплитудно-фазовую характеристику на комплексной плоскости трудно. В этом уравнении две переменных величины: частота ω, которую изменяем от 0 до ∞ и амплитуда входного сигнала на нелинейного элемента А, который определяется по Wл.ч(jω). Л.С. Гольдфарб предложил это уравнение представить в виде

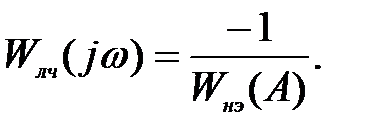
Автоколебания в системе возможны, если выполняются два условия гармонического баланса

.

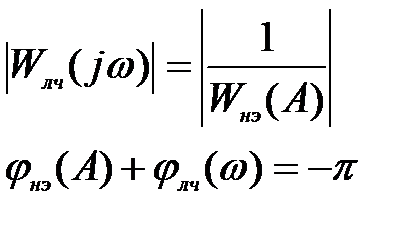Первое условие. Отдельно построенная левая часть уравнения при изменении частоты и отдельно построенная правая часть уравнения при изменении амплитуды имеют общую точку пересечения (в некоторых случаях несколько точек пересечения).

Второе условие. Точки пересечения соответствуют суммарному фазовому сдвигу на угол -π (радиан) или минус 180⁰.

Таким образом, колебательный процесс в системе возможен, если есть точки пересечения амплитудных характеристик и выполняется требование к фазовым характеристикам (рис. 2.27).

Полученные уравнения проще всего решать графо-аналитически. Очевидно, что если эти два годографы на комплексной плоскости не пересекаются, то они не имеют общего решения, и в исследуемой системе нет колебательного процесса (рисунок 2.27 а). Если эти годографы пересекаются, то есть общее решение в исследуемой системе и есть колебательный процесс (рисунок 2.27 б). Если эти годографы пересекаются в двух точках, то в исследуемой системе есть два вида колебательных процесса. Из них один вид или с амплитудой А1 – неустойчивый колебательный процесс, а второй вид или с амплитудой А2 – устойчивый колебательный процесс (рис. 2.28 в).

Рис.2.27. К определению частоты и амплитуды автоколебаний

Об устойчивости или неустойчивости колебательного процесса судят следующим образом. Пусть годографы пересекаются в точке А1 при частоте ω0 и амплитуде А0 (рисунок 2.27 в). Зададим некоторые приращение ΔА. Для устойчивости автоколебаний требуется, чтобы при А1 +ΔА колебания становились затухающие и амплитуда возвращалась к А1. При А1 – ΔА колебания становились возрастающие и амплитуда тоже возвращается к А1.

Если при А1 +ΔА амплитуда начала возрастать, а при А1 – ΔА она стала

убывать, то возникший предельный цикл неустойчивый.

Контрольные вопросы для самопроверки

1. Какой сигнал считается центрированным?

2. Как определяется передаточная функция нелинейного звена?

3. Почему у нелинейного звена передаточная функция называется гармонической?

4. Чему равна передаточная функция нелинейного звена с зоной нечувствительности при A<a?

5. Как получается гармоническая частотная передаточная функция нелинейного звена?

6. Как можно математически через коэффициенты q(A) и q’(A) определить величину запаздывания?

7. С увеличением амплитуды входного сигнала величина запаздывания в нелинейных звеньях с петлей гистерезиса увеличивается или уменьшается?

8. С увеличением частоты входного сигнала величина запаздывания в однозначных нелинейных звеньях увеличивается или уменьшается?