2014-02-02
42078
Если изменять угловую частоту ω входного сигнала от 0 до ∞, то вектор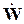 
на комплексной плоскости будет изменяться по модулю и поворачиваться относительно вещественной оси.
Амплитудно-фазовой характеристикой называют линию (годограф), вычерчиваемую на комплексной плоскости вектором частотной функции при изменении угловой частоты ωвходного сигнала от 0 до ∞.
АФХ показывает относительное изменение амплитуды и фазы гармонического сигнала, передаваемого звеном или системой при изменении угловой частоты ω от 0 до ∞.
В качестве примерарассмотрим комплексную частотную передаточную функцию и амплитудно-фазовую характеристику апериодического звена первого порядка, которое характеризуется следующим уравнением:
.
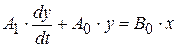преобразуем уравнение:
,
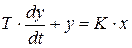где Т – постоянная времени;
К – коэффициент усиления.
; 
.
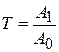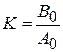Используя преобразование Лапласа, получаем:
T × p × y (р) + y (р) = K × x (р),
или
y (р) (1 + T ×p)× = K × x (р).
Для получения формулы комплексной частотной передаточной функции надо разрешить это уравнение относительно выходного сигнала и разделить на входной сигнал:
|
|
|
,
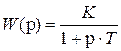или
.
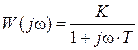Для определения амплитудно-фазовой характеристики, комплексную частотную передаточную функцию необходимо представить в виде суммы вещественной и мнимой частей:
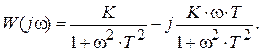
Зависимость модуля передаточной функции от угловой частоты определяет амплитудно-частотную характеристику (АЧХ), а зависимость фазы передаточной функции определяет фазо-частотную характеристику (ФЧХ) звена:
,
.
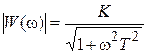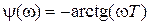Выразив величину ω Т из второго уравнения и подставив его в уравнение АФХ, получим выражение модуля частотной передаточной функции через фазу:
ω Т = tg (ψ(ω));
.
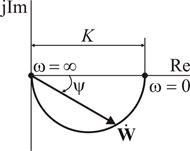
Из полученного выражения следует, что АФХ апериодического звена первого порядка представляет собой полуокружность, диаметр которой расположен на вещественной оси и соответствует коэффициенту усиления К апериодического звена. При увеличении частоты модуль вектора частотной функции звена уменьшается вследствие поворота вектора передаточной функции против часовой стрелки. При бесконечно большой частоте модуль вектора стремится к нулю, а фаза достигает – 90º.
Логарифмические частотные характеристики (ЛЧХ).
Комплексную частотную передаточную функцию при изменении угловой частоты можно представить двумя вещественными характеристиками: амплитудно-частотной и фазо-частотной. Недостатками этих характеристик является сложность их представления в широком диапазоне изменения угловой частоты. Расчет и построение этих характеристик существенно упрощается при использовании логарифмических масштабов.
|
|
|
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) показывает, как изменяется в логарифмическом масштабе в зависимости от угловой частоты амплитуда гармонического сигнала, передаваемого звеном или системой относительно амплитуды входного гармонического сигнала. Для количественного выражения ординат ЛАЧХ использована логарифмическая единица усиления мощности гармонического сигнала 1бел [Б], применяемая в акустике.
Логарифмическая единица усиления мощности 1бел [Б], характеризует усиление мощности сигнала в 10 раз. Мощность гармонического сигнала пропорциональна квадрату его амплитуды, поэтому 1 Б соответствует усиление амплитуды сигнала в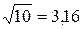 
раза. Практически используют дольную единицу 1 децибел [дБ] = 0,1 Б, соответствующую усилению мощности сигнала в 
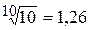раза и увеличению амплитуды в 
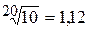раза.
Логарифмы угловой частоты lgω выражаются в декадах; 1 дек соответствует увеличению частоты в 10 раз, lgω = 0 соответствует ω = 1 с-1.
Аналитическое выражение ЛАЧХ G (ω) определяется логарифмированием квадрата модуля комплексной частотной функции и умножением на 10 для перевода в дольные единицы усиления мощности – децибелы:
.
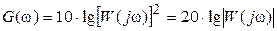График ЛАХЧ строят в логарифмических координатах. Усиление мощности сигнала, в децибелах, откладывают по оси ординат, а логарифмическое увеличение частоты, в декадах – по оси абсцисс. Расположение характеристики выше ординат характеризует усиление амплитуды и мощности гармонического сигнала на выходе звена или системы относительно входного. Если характеристика или ее часть расположена ниже оси абсцисс, это соответствует ослаблению амплитуды и мощности сигнала. В точке пересечения характеристикой оси абсцисс, называемой частотой среза ωср.
ω = ωср;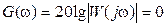 
Þ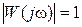 
.
Термин "частота среза " обозначает частоту гармонического сигнала, выше которой амплитуда сигнала на выходе звена или системы становится меньше, чем на входе (происходит срезание амплитуды и мощности сигнала).
Логарифмическая фазо-частотная характеристика (ЛФЧХ) – это зависимость относительного изменения фазы гармонического сигнала при передаче его звеном или системой от логарифма угловой частоты. На графике изменение фазы ψ, выраженное в угловых градусах или радианах, откладывают по оси ординат. Логарифмическую частоту, в декадах, откладывают по оси абсцисс. Логарифмические амплитудно- и фазо-частотные характеристики обычно совмещают по координате lgw, или располагают одну под другой.
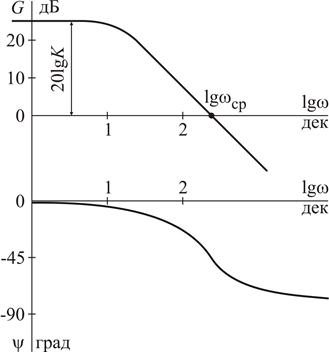
Изображение характеристик в логарифмических координатах имеет по сравнению с обычными частотными характеристиками следующие преимущества:
1. Форма логарифмических частотных характеристик не зависит от параметров звена: коэффициента усиления и постоянной времени; форма характеристик определяется формулой частотной передаточной функции.
2. ЛАЧХ смещается по оси ординат вверх при увеличении коэффициента усиления звена, вниз – при уменьшении коэффициента усиления.
3. ЛАЧХ и ЛФЧХ смещаются по оси абсцисс влево при увеличении постоянной времени звена, вправо – при уменьшении постоянной времени.
Использование характеристик типовых звеньев сводит все расчеты характеристик к вычислению двух координат: логарифма коэффициента усиления и логарифма величины, обратной постоянной времени, называемой частотой сопряжения либо частотой среза. Частота сопряжения характеристики звена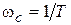 
определяет расположение характеристик на оси абсцисс. Обычно построение ЛАХЧ выполняют упрощенным способом, заменяя действительные характеристики линейными отрезками. При построении ЛФХЧ используют шаблоны.
