Вычислим площадь плоской фигуры, ограниченной графиком непрерывной, неотрицательной функции y=f(x), прямыми x=a, x=b, отрезком [ a,b ]. Такая фигура называется криволинейной трапецией.
1) Разобьем отрезок [ a, b ] произвольным образом на n частей точками 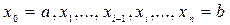 . Получим n маленьких отрезков с длинами
. Получим n маленьких отрезков с длинами 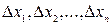 ;
; 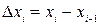 .
.
2) Через точки деления проведем вертикальные прямые. Трапеция разобьется на n трапеций. На каждом из элементарных отрезков выберем произвольным образом по точке 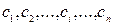 .
.
Найдем значения функции в этих точках
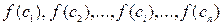 .
.
Примем эти ординаты за высоты прямоугольников.
3) Посчитаем, что площади маленьких криволинейных трапеций приближенно равны площадям прямоугольников с основаниями 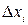 и высотами
и высотами 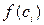 . Тогда
. Тогда
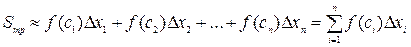 .
.
Чем мельче отрезки деления, тем точнее это равенство. За точное значение площади трапеции примем предел, к которому стремятся площади ступенчатых фигур при неограниченном увеличении числа отрезков деления и стремлении к нулю наибольшей из длин этих отрезков.
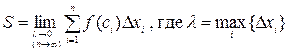 .
.
 2015-02-18
2015-02-18 528
528








