Если относительно данной переменной интеграл не является табличным, то в некоторых случаях его можно привести к табличному относительно новой переменной с помощью подведения под знак дифференциала нужной функции.
При этом удобно пользоваться следующими формулами, которые получаются из формул дифференцирования при прочтении их в обратном порядке:
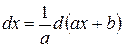
| 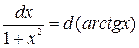
|
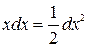
| 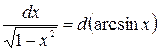
|
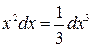
| 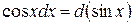
|
| … | 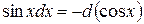
|
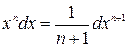 , n ≠-1 , n ≠-1
| 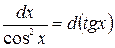
|
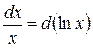
| 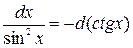
|
Примеры (см. задание 1а)
1) 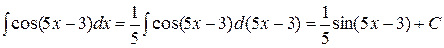 ;
;
2) 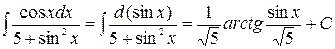
3) 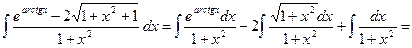
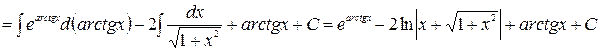
 2015-02-18
2015-02-18 329
329








