Случайной величиной называют такую величину, которая в результате испытания принимает одно и только одно из возможных своих значений, заранее неизвестное и зависящее от случайных обстоятельств, которые не всегда можно учесть. Обозначается X, Y, Z, …, возможные ее значения обозначаются 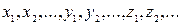 .
.
Случайные величины бывают дискретные и непрерывные. Дискретная случайная величина принимает отдельные изолированные возможные значения с определенными вероятностями.
Соответствие между возможными значениями дискретной случайной величины и их вероятностями называется законом или рядом распределения.
Пример. Бросаем игральную кость. Случайная величина X – число выпавших очков, ее возможные значения 1, 2, 3, 4, 5, 6. Любое из этих значений появляется с вероятностью 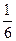 . Тогда:
. Тогда:
| X | ||||||
| P | 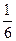
| 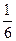
| 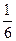
| 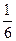
| 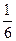
| 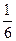
|
– ряд распределения случайной величины.
Так как в каждом испытании случайная величина обязательно примет одно из возможных своих значений, то события 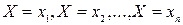 образуют полную группу попарно несовместных событий, а поэтому
образуют полную группу попарно несовместных событий, а поэтому 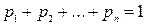 .
.
Пример (см. задание 8). Составить закон распределения числа отказавших элементов прибора, если элементов три, а вероятность отказа каждого, независимо работающего элемента равна 0,2.
Пусть случайная величина X – число отказавших элементов, ее возможные значения:
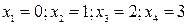 ,
,
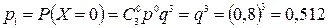 ,
,
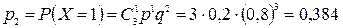 ,
,
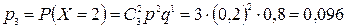 ,
,
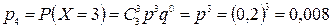 .
.
Тогда закон распределения этой случайной величины принимает вид:
| X | ||||
| P | 0,512 | 0,384 | 0,096 | 0,008 |
Контроль: 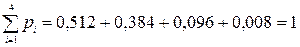
 2015-02-18
2015-02-18 475
475







