2015-02-18
342
При большой выборке, отобранной из генеральной совокупности нормального распределения, предполагается считать распредение коэффициента корреляции близко к нормальному со средней, равной «r» и дисперсией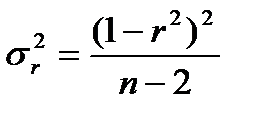 
, а среднеквадратическая ошибка коэффициента корреляции тогда будет равна:
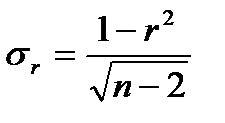, где
r – коэффициент корреляции выборочной совокупности;
n – объем выборки;
k = n – 2 – число степеней свободы при линейной зависимости.
Если величина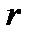 
> 
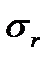в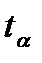 
раз, или 
> 
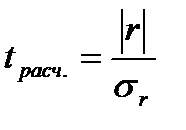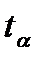[8]
Найдем для сгруппированных данных (см. таб. 14) среднюю квадратическую ошибку коэффициента корреляции:
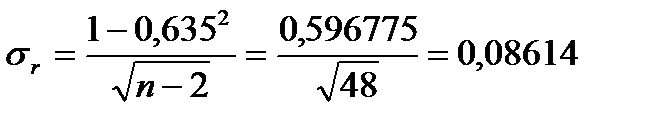, тогда
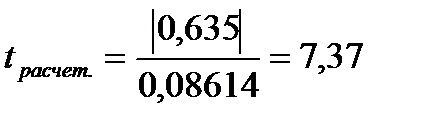
С вероятностью0,95 и числом степеней свободы k = 50 – 2 = 48,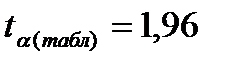 
[9].
Поскольку 
> 
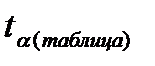, следует, что с вероятностью Р = 0,95 и числом степеней свободы k = 48 можно утверждать о существенности выборочного коэффициента корреляции, т.е. связь между х и y – значимая.
Для генеральной совокупности коэффициент корреляции будет находится в пределах.
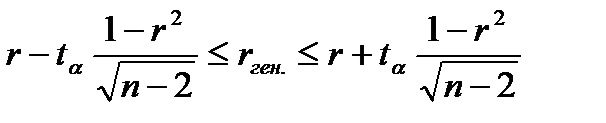
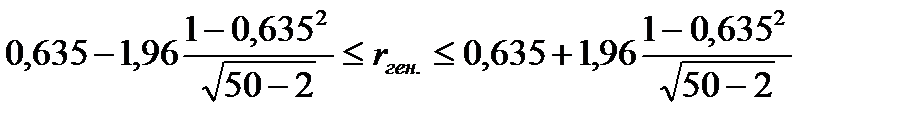
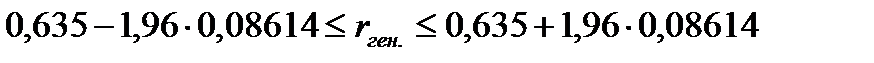
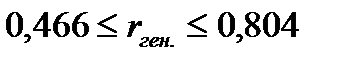
или
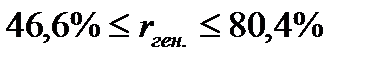
С вероятностью 0,95 можно утверждать, что коэффициент корреляции будет не ниже 46,6% и не выше 80,4%.
