При малой выборки

Для малого объема выборочной совокупности 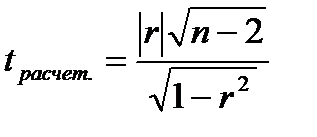для оценки значимости коэффициента корреляции.

Если > 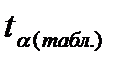, то расчетный коэффициент корреляции существенен и связь между х и y вполне реальна. Если < 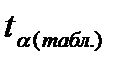, то связь между х и y несущественна и корреляционная связь в генеральной совокупности отсутствует.

По данным таблицы 15

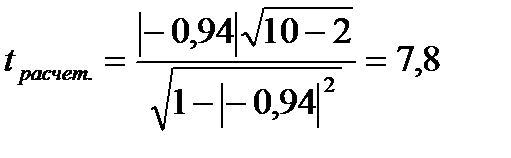, а с вероятностью 0,95 и числом степеней свободы k = 10 – 2 = 8, 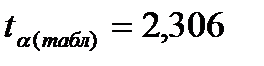[10].

Значит связь между х (простоями) и y – (выпуском продукции) существенна, т.к.

>

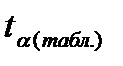
8. Проверка возможности использования прямолинейной функции – гипотезы Кендэла [11] о линейной корреляционной зависимости.

Для проведения гипотезы Кендэла о линейной зависимости определяется величина вероятности, которая рассчитывается по следующей формуле:

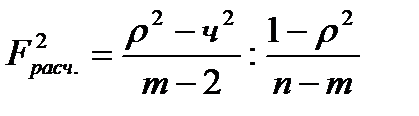[12], где

n – объем совокупности

m – число групп по признаку фактору х

Если критерий 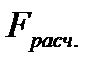найденный с определенной вероятностью и критериями свободы ( 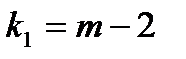и 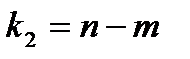) будут меньше F расчетного, то гипотеза о линейной связи между х и у отвергается. Если наоборот – то возможность использовать линейную функцию не опровергается.

По данным таблицы 14 рассчитаем этот критерий.

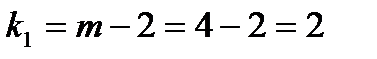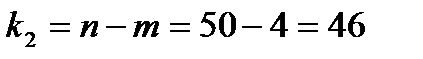Критерий свободы , а . С вероятностью 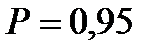, 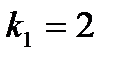и 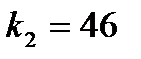табличное значение 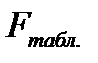- критерия [13] = 3,2.

Расчетный критерий равен:

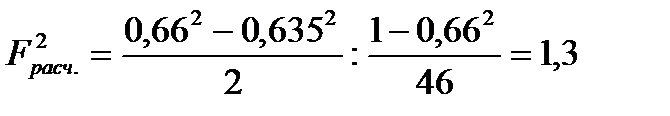
Поскольку 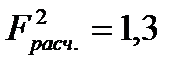меньше 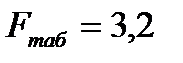, то это не позволяет отклонить гипотезу о линейной связи между производительностью труда – х и товарной продукцией – y.

Вопросы для самопроверки

1. Что такое функциональные и корреляционные связи?

2. Какие задачи стоят перед корреляционным анализом?

3. Назовите виды корреляционной зависимости и рассмотрите их.

4. Как графически изображается корреляционная зависимость для несгруппированных и сгруппированных данных?

5. Эмпирическая линия регрессии и её характеристика.

6. Теоретическая линия регрессии и её характеристика.

7. Показатели тесноты связи и их характеристика.

8. Сущность коэффициента корреляции.

9. Характеристика эмпирического корреляционного отношения.

10. Теоретическое корреляционное отношение и его характеристика.

11. Простейшие показатели тесноты связи: коэффициент Фехнера, коэффициент корреляции рангов, коэффициент ассоциации.

12. Методы оценки существенности расчета коэффициента корреляции.

13. Гипотеза Кендела о линейной корреляционной зависимости.