Многократные измерения необходимо проводить в тех случаях, когда имеются случайные погрешности. Эти погрешности следует рассматривать как случайные события по теории вероятностей. Случайными называются события, появление которых невозможно предусмотреть. Случайные события имеют вероятность между 0 и 1. Ноль соответствует невозможному событию, единица – достоверному, которое происходит обязательно.
Случайные величины могут быть как дискретными, так и непрерывными. Дискретные величины – это только целые числа. Например, число годных или бракованных деталей. Непрерывные величины – это любые значения на числовой оси. Например, действительные размеры обрабатываемых деталей.
Случайные величины могут подчиняться одному из следующих законов распределения:
- нормальный закон, описывающий случайные величины, которые имеют место при большом числе одновременно действующих переменных факторов;
- закон равной вероятности, описывающий непрерывные случайные величины, которые достоверно встречаются на некотором интервале от а до b и вероятность наблюдения случайной величины в этом интервале постоянна (движение секундной стрелки часов и отсчет времени);
- закон Максвелла, или закон существенно положительных величин, используемый для определения погрешностей эксцентриситета и формы поверхностей;
- закон треугольника (Симпсона) и другие.
Результаты измерений могут содержать как систематические, так и случайные погрешности. Выясненные систематические погрешности необходимо устранить. Например, проверить годность средства измерений, промыть и очистить контролируемую деталь и т.д.
Свойства случайной величины описываются законом распределения, который устанавливает связь между возможными значениями случайной величины и соответствующими им вероятностями. Функция распределения случайных величин является дифференцируемой функцией, поэтому чаще используют ее первую производную, которую называют плотностью распределения.
Плотность распределения – неотрицательная функция, т.е. кривая распределения всегда лежит выше оси абсцисс (рис.5).
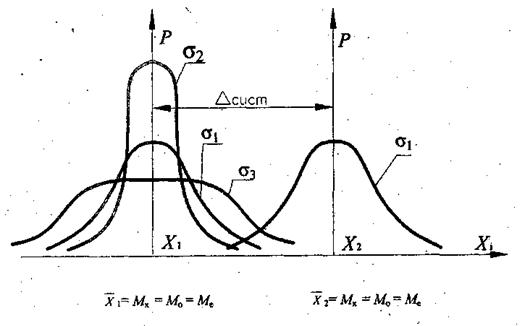 |
Рис.5. Кривые плотности распределения при разных значениях 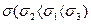
и при наличии систематической погрешности
Аксиомы теории вероятностей:
· аксиома случайностей – число положительных событий равно числу отрицательных событий, т.е. площади под кривой распределения справа и слева от оси ординат равны 0,5;
· аксиома распределения – малые по модулю значения случайных событий встречаются чаще, чем большие, т.е. кривая имеет колоколообразную форму и асимптотически приближается к оси абсцисс.
При изучении свойств случайной величины используют их числовые характеристики, которые выражают наиболее существенные особенности распределения. Центр группирования случайной величины оценивается следующими характеристиками:
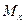 - математическое ожидание – это среднее значение случайной величины; т.е. среднее арифметическое значение, обозначаемое
- математическое ожидание – это среднее значение случайной величины; т.е. среднее арифметическое значение, обозначаемое 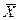 . Среднее арифметическое значение определяется суммированием всех результатов наблюдений и делением этой суммы на число выполненных наблюдений. Эта величина наибольшим образом приближается к истинному значению:
. Среднее арифметическое значение определяется суммированием всех результатов наблюдений и делением этой суммы на число выполненных наблюдений. Эта величина наибольшим образом приближается к истинному значению:
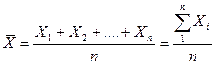 ; (5)
; (5)
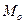 - мода случайной величины – это такое значение случайной величины, в котором плотность вероятности имеет максимальное значение, это значение наиболее часто встречается в рассматриваемом статистическом ряду;
- мода случайной величины – это такое значение случайной величины, в котором плотность вероятности имеет максимальное значение, это значение наиболее часто встречается в рассматриваемом статистическом ряду;
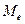 - медиана (центр симметрии) случайной величины – это такое значение случайной величины, которое делит площадь под кривой распределения на равновеликие участки, медиана занимает среднее значение в статистическом ряду. При нечетном числе измерений медианой будет среднее значение, а при четном числе измерений медиана определяется как полусумма двух значений, расположенных в середине ряда.
- медиана (центр симметрии) случайной величины – это такое значение случайной величины, которое делит площадь под кривой распределения на равновеликие участки, медиана занимает среднее значение в статистическом ряду. При нечетном числе измерений медианой будет среднее значение, а при четном числе измерений медиана определяется как полусумма двух значений, расположенных в середине ряда.
Для нормального закона часто среднее арифметическое значение совпадает с математическим ожиданием, модой и медианой случайной величины (рис.5).
Мерой рассеивания случайных величин выступают:
· дисперсия 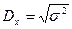 , она характеризует рассеивание случайной величины относительно ее математического ожидания;
, она характеризует рассеивание случайной величины относительно ее математического ожидания;
· среднее квадратичное отклонение (СКО) случайной величины - 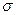 , мкм; СКО имеет такую же размерность, как исследуемая случайная величина:
, мкм; СКО имеет такую же размерность, как исследуемая случайная величина:
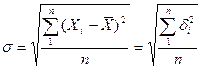 , (6)
, (6)
где 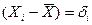 - абсолютная погрешность i -го результата (отклонение от среднего значения).
- абсолютная погрешность i -го результата (отклонение от среднего значения).
Чтобы перейти от учета индивидуальных признаков случайных событий к универсальному выражению, пользуются нормированным отклонением t и функцией Лапласа 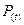 (функция нормального распределения):
(функция нормального распределения):
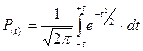 , (7)
, (7)
где e =2,718 - основание натуральных логарифмов, t – нормированное отклонение, безразмерный коэффициент, равный
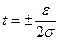 , (8)
, (8)
где ε - доверительный интервал для случайных величин от –t до +t, который оценивается по формуле:
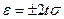 . (9)
. (9)
Форма кривой нормального распределения (рис.5) зависит от значения среднего квадратичного отклонения 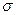 .
.
При малых значениях 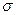 кривая идет более круто и имеет большее значение по оси ординат. При больших значениях
кривая идет более круто и имеет большее значение по оси ординат. При больших значениях 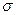 кривая вытягивается вдоль оси абсцисс. При этом площади под кривыми с разными значениями
кривая вытягивается вдоль оси абсцисс. При этом площади под кривыми с разными значениями 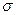 одинаковые.
одинаковые.
При изменении центра группирования кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы, так как действует систематическая погрешность.
Вся площадь, ограниченная кривой распределения и осью абсцисс, равна 1. Вероятность того, что значение дискретной случайной величины принадлежит некоторому интервалу от 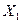 до
до 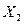 , определяется как разность значений функции распределения на границах этого интервала, т.е. равна площади под кривой распределения, опирающейся на этот интервал.
, определяется как разность значений функции распределения на границах этого интервала, т.е. равна площади под кривой распределения, опирающейся на этот интервал.
Следует вывод: чем больше доверительный интервал, тем больше доверительная вероятность.
Характерные точки для интервалов:
- интервал в 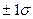 имеет вероятность Р=0,68;
имеет вероятность Р=0,68;
- интервал в 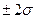 - вероятность Р=0,95;
- вероятность Р=0,95;
- интервал в 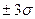 - вероятность Р=0,997.
- вероятность Р=0,997.
Для практических целей часто используют интервал в 6 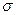 ,т.е. допуск на изготовление должен соответствовать интервалу в 6 σ (рис.6).
,т.е. допуск на изготовление должен соответствовать интервалу в 6 σ (рис.6).
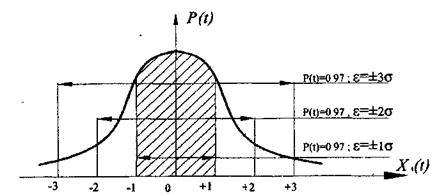 |
Рис.6. Зависимость доверительной вероятности от доверительного интервала
Числовые значения функции Лапласа (вероятности) для некоторых значений нормированного отклонения представлены в таблице учебного пособия [4]. Число измерений n влияет на вероятность результата. При числе измерений n< 20расчеты по нормальному закону могут дать большую погрешность. В этом случае рекомендуется использовать закон Стьюдента (псевдоним английского математика и химика В.С. Госсета).
Для оценки случайных событий практически часто применяют закон Стьюдента. Значения доверительной вероятности 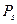 при разных значениях коэффициента Стьюдента и числа измерения n даны в табл.1.Часто требуется найти ts по известным
при разных значениях коэффициента Стьюдента и числа измерения n даны в табл.1.Часто требуется найти ts по известным 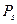 и n (табл.2).
и n (табл.2).
По закону Стьюдента значение 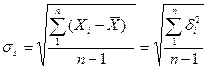 (10)
(10)
Табл.1. Значения доверительной вероятности 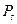 для различных значений
для различных значений 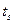 и числа измерений n (распределение Стьюдента)
и числа измерений n (распределение Стьюдента)
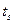 | 2,5 | 3,5 | ||
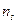 | ||||
| 0,705 | 0,758 | 0,795 | 0,823 | |
| 0,816 | 0,870 | 0,905 | 0,928 | |
| 0,861 | 0,912 | 0,942 | 0,961 | |
| 0,884 | 0,933 | 0,960 | 0,975 | |
| 0,898 | 0,946 | 0,970 | 0,983 | |
| 0,908 | 0,953 | 0,976 | 0,987 | |
| 0,914 | 0,959 | 0,980 | 0,990 | |
| 0,919 | 0,963 | 0,983 | 0,992 | |
| 0,923 | 0,966 | 0,985 | 0,993 | |
| 0,927 | 0,969 | 0,987 | 0,994 | |
| 0,929 | 0,970 | 0,988 | 0,995 | |
| 0,931 | 0,972 | 0,989 | 0,996 | |
| 0,933 | 0,974 | 0,990 | 0,996 | |
| 0,935 | 0,974 | 0,990 | 0,996 | |
| 0,936 | 0,975 | 0,991 | 0,997 | |
| 0,937 | 0,976 | 0,992 | 0,997 | |
| 0,938 | 0,977 | 0,992 | 0,997 |
Табл. 2. Коэффициент Стьюдента 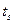 для различных значений доверительной вероятности
для различных значений доверительной вероятности 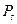 и числа n
и числа n
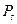 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | 0,999 |
| n | |||||||||
| 1,000 | 1,376 | 1,963 | 3,08 | 6,31 | 12,71 | 31,8 | 63,7 | 63,7 | |
| 0,816 | 1,061 | 1,336 | 1,886 | 2,92 | 4,30 | 6,96 | 9,92 | 31,6 | |
| 0,765 | 0,978 | 1,250 | 1,638 | 2,35 | 3,18 | 4,54 | 5,84 | 12,94 | |
| 0,741 | 0,941 | 1,190 | 1,533 | 2,13 | 2,77 | 3,75 | 4,60 | 8,61 | |
| 0,727 | 0,920 | 1,156 | 1,476 | 2,02 | 2,57 | 3,36 | 4,03 | 6,86 | |
| 0,718 | 0,906 | 1,134 | 1,440 | 1,943 | 2,45 | 3,14 | 4,71 | 5,96 | |
| 0,711 | 0,896 | 1,119 | 1,415 | 1,895 | 2,36 | 3,00 | 3,5 | 5,40 | |
| 0,706 | 0,889 | 1,108 | 1,397 | 1,860 | 2,31 | 2,90 | 3,36 | 5,04 | |
| 0,703 | 0,883 | 1,110 | 1,383 | 1,833 | 2,26 | 2,82 | 3,25 | 4,78 | |
| 0,700 | 0,879 | 1,093 | 1,372 | 1,812 | 2,23 | 2,76 | 3,17 | 4,59 | |
| 0,697 | 0,876 | 1,088 | 1,363 | 1,796 | 2,20 | 2,72 | 3,11 | 4,49 | |
| 0,695 | 0,873 | 1,083 | 1,356 | 1,782 | 2,18 | 2,68 | 3,06 | 4,32 | |
| 0,694 | 0,870 | 1,079 | 1,350 | 1,771 | 2,16 | 2,65 | 3,01 | 4,22 | |
| 0,692 | 0,868 | 1,076 | 1,345 | 1,761 | 2,14 | 2,62 | 2,98 | 4,14 | |
| 0,691 | 0,866 | 1,074 | 1,341 | 1,753 | 2,13 | 2,60 | 2,95 | 4,07 | |
| 0,690 | 0,865 | 1,071 | 1,337 | 1,746 | 2,12 | 2,58 | 2,92 | 4,02 | |
| 0,689 | 0,863 | 1,069 | 1,333 | 1,740 | 2,11 | 2,57 | 2,90 | 3,96 | |
| 0,688 | 0,862 | 1,067 | 1,330 | 1,734 | 2,10 | 2,55 | 2,88 | 3,92 | |
| 0,688 | 0,861 | 1,066 | 1,328 | 1,729 | 2,09 | 2,54 | 2,86 | 3,88 | |
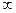 | 0,674 | 0,842 | 1,036 | 1,282 | 1,645 | 1,96 | 2,53 | 2,58 | 3,29 |
Случайные факторы (погрешности) оцениваются двумя числами:
- доверительной вероятностью (степенью надежности) 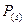 ;
;
- доверительным интервалом 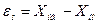 .
.
Доверительный интервал для закона Стьюдента определяется по следующей формуле:
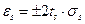 . (11)
. (11)
Следовательно, 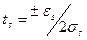 , (12)
, (12)
т.е. это безразмерный коэффициент Стьюдента.
Интервал для среднего арифметического значения определяется с учетом среднего квадратического отклонения среднего арифметического по формуле (13) или (14):
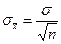 ; (13)
; (13)
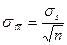 . (14)
. (14)
Погрешность среднего арифметического в несколько раз меньше погрешности каждого результата и интервал для него определяется по следующим зависимостям:
- для нормального закона 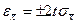 ; (15)
; (15)
- для закона Стьюдента 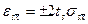 . (16)
. (16)
После обработки результатов измерений, содержащих случайные погрешности, ответ должен быть представлен в следующем виде:
- для закона Стьюдента 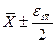 при
при 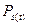 или
или
- для нормального закона 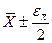 при
при 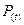 ,
,
т.е. необходимо указать среднее арифметическое значение, интервал, в котором он находится, и вероятность попадания в этот интервал.
Окончательный результат измерения должен быть округлен, так как лишние знаки дают ложное представление о высокой точности результата.
 2015-02-24
2015-02-24 5209
5209
