Рассмотрим уравнение с тремя переменными 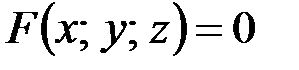 , и предположим, что оно определяет в некоторой области
, и предположим, что оно определяет в некоторой области 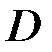 плоскости
плоскости 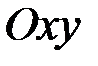 неявную функцию
неявную функцию 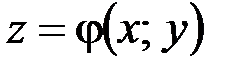 , так что имеет место тождество
, так что имеет место тождество 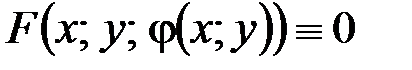 .
.
Теорема (существования неявной функции). Пусть функция 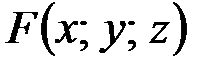 непрерывна вместе со своими частными производными в некоторой окрестности точки
непрерывна вместе со своими частными производными в некоторой окрестности точки 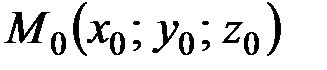 . Если
. Если 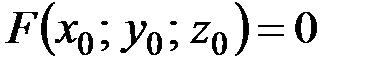 , а
, а 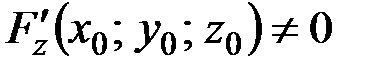 , то существует окрестность точки
, то существует окрестность точки 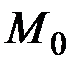 , в которой уравнение
, в которой уравнение 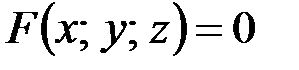 определяет
определяет 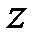 как однозначную непрерывную и имеющую непрерывные частные производные функцию от
как однозначную непрерывную и имеющую непрерывные частные производные функцию от 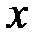 и
и 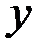
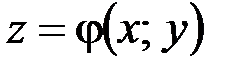 , такую что
, такую что 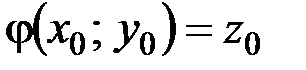 .
.
Замечание. Если в точке 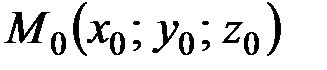 производная
производная 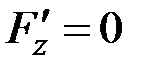 , а, например,
, а, например, 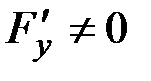 , то уравнение
, то уравнение 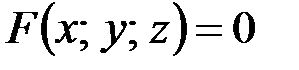 может не определять
может не определять 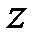 как функцию от
как функцию от 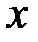 и
и 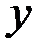 , но определяет
, но определяет 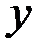 как функцию от
как функцию от 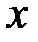 и
и 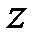 .
.
Частные производные такой функции вычисляются по формулам:
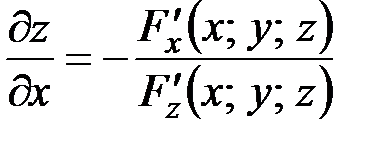 ,
, 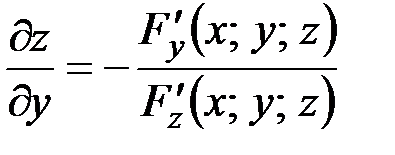 при
при 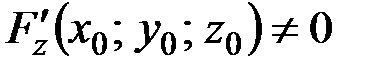 .
.
Если уравнение 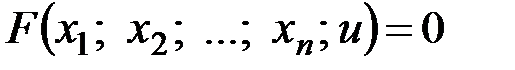 определяет
определяет 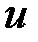 как некоторую функцию от
как некоторую функцию от 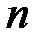 независимых переменных величин
независимых переменных величин 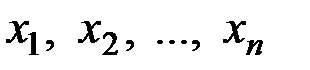 , то ее частные производные по переменным
, то ее частные производные по переменным 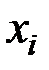 находятся по формулам:
находятся по формулам: 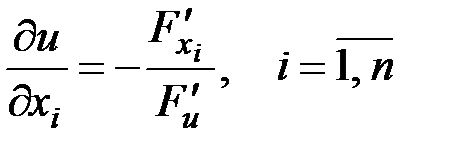 .
.
Пример. Найти частные производные функции 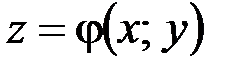 , заданной неявно:
, заданной неявно: 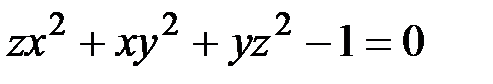 .
.

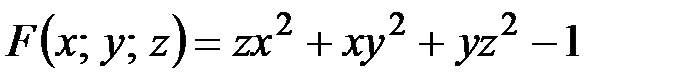 . Найдем частные производные функции
. Найдем частные производные функции 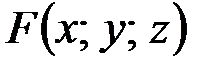 :
: 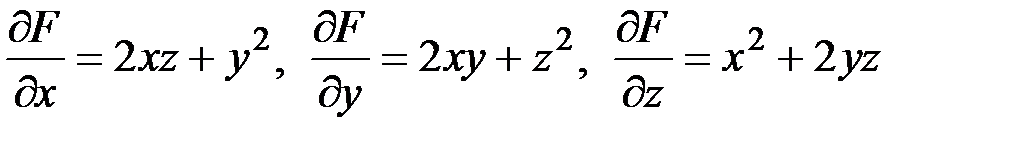 , тогда
, тогда
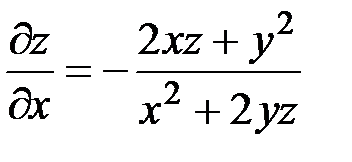 ,
, 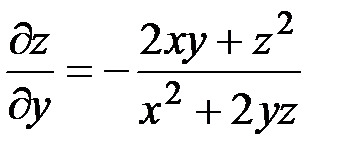 .
. 
 2015-02-24
2015-02-24 374
374







