2015-02-24
354
I. Пусть функция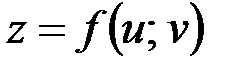 
определена, непрерывна и имеет непрерывные частные производные в области 
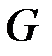плоскости 
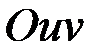, а функци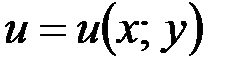и 
и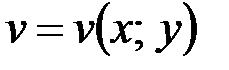 
определены, непрерывны и имеют непрерывные частные производные в области 
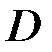плоскости 
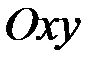; причем, если 
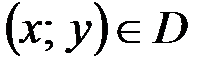, то соответствующая точка 
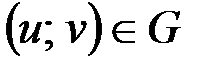. Тогда переменную 
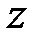можно рассматривать как сложную функцию независимых переменных 
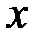и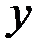 
в области : 
.
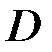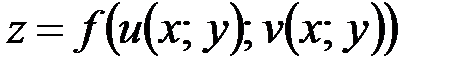Тогда справедливы формулы дифференцирования данной сложной функции:
, 
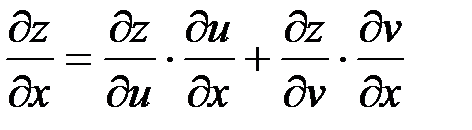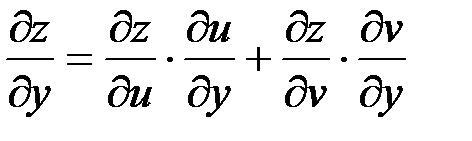. (1)
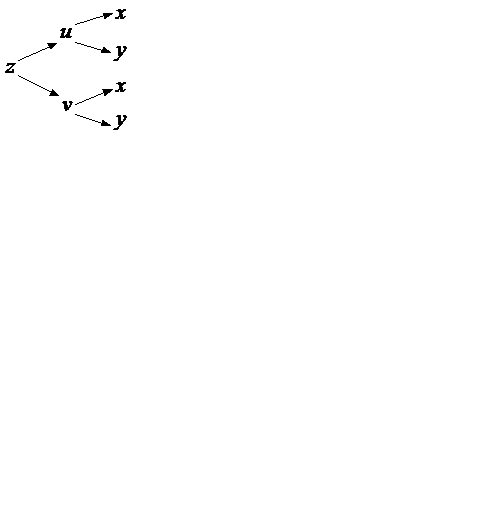
– графическая схема дифференцирования.
Пример. Найти частные производные функции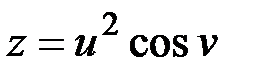 
, если 
, 
.
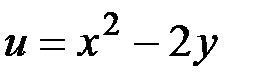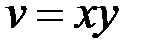Найдем частные производные данных функций: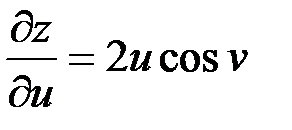 
, 
; 
, 
; 
, 
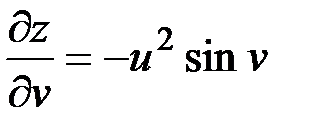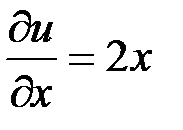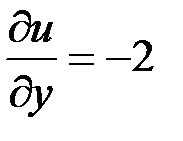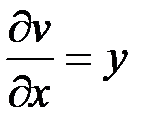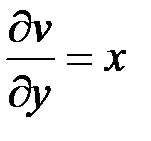и подставим их в формулы (1):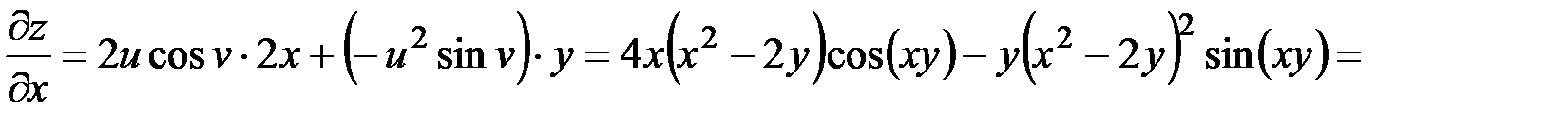 
,
. 
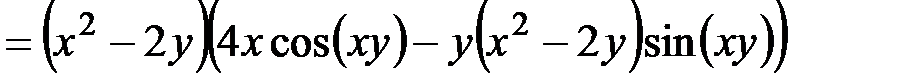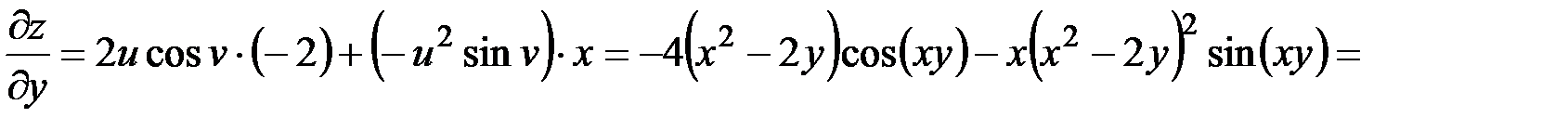
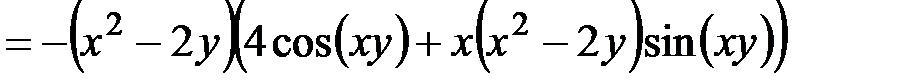II. Пусть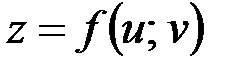 
– сложная функция, где 
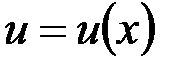и 
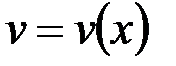– функции одного аргумента 
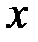. Тогда функцию 
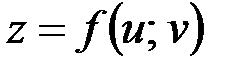можно рассматривать как функцию одной независимой переменной и находить производную 
:
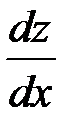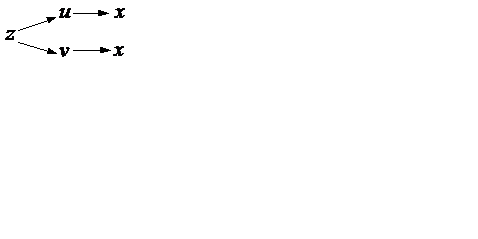
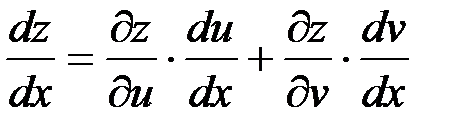. (2)
Графическая схема дифференцирования:
Пример. Найти частные производные функции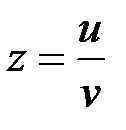 
, если 
, 
.
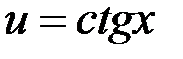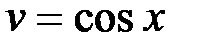Найдем частные производные данных функций: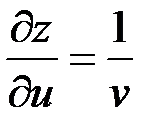 
, 
; 
; 
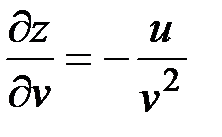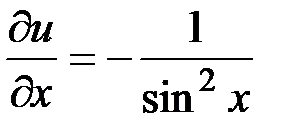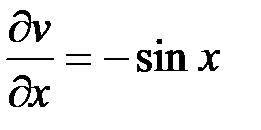и подставим их в формулу (2):
. 
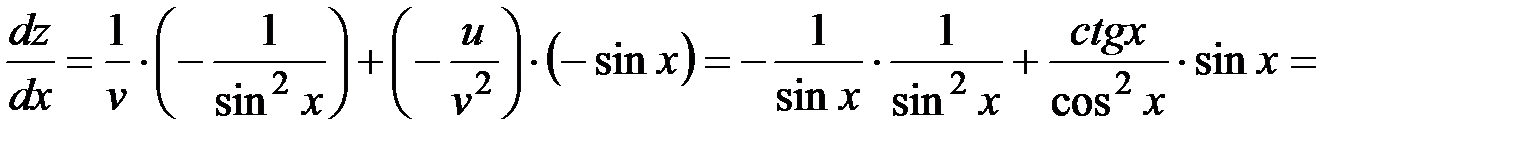
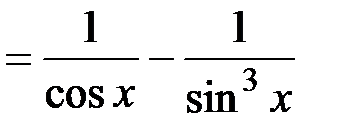Рассмотренные правила дифференцирования сложной функции справедливы для функций любого числа независимых переменных.
