Пусть в некоторой области 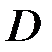 задана функция двух переменных
задана функция двух переменных 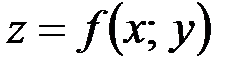 . Возьмем произвольную точку
. Возьмем произвольную точку 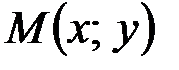 этой области и дадим х приращение
этой области и дадим х приращение 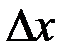 , а значение
, а значение 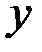 оставим неизменным. При этом функция
оставим неизменным. При этом функция 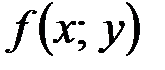 получит частное приращение по
получит частное приращение по 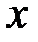 :
: 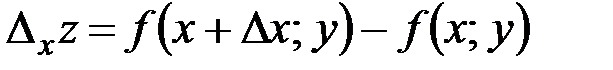 .
.
Опр. Частной производной функции 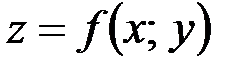 по переменной
по переменной 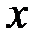 в точке
в точке 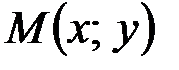 называется предел (если он существует) отношения соответствующего частного приращения
называется предел (если он существует) отношения соответствующего частного приращения  к вызвавшему его приращению
к вызвавшему его приращению 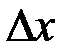 при
при 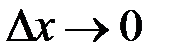 :
: 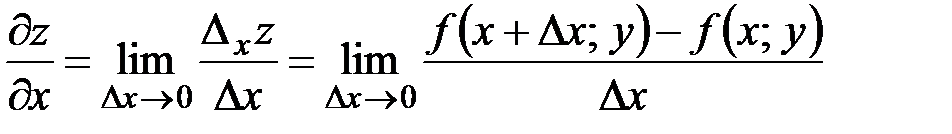 .
.
Обозначение: 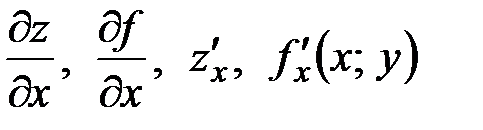 .
.
Аналогично вводится понятие частного приращения функции 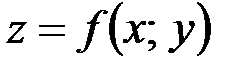 по
по 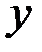 :
: 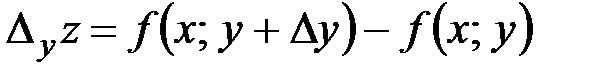 , а частная производная функции
, а частная производная функции 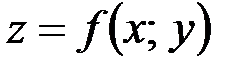 по переменной
по переменной 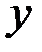 в точке
в точке 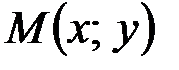 определяется как предел (если он существует) отношения соответствующего частного приращения
определяется как предел (если он существует) отношения соответствующего частного приращения 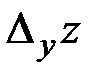 к вызвавшему его приращению
к вызвавшему его приращению 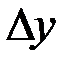 при
при 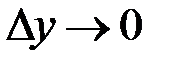 :
: 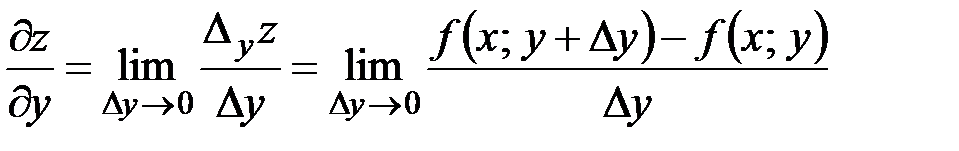 .
.
Обозначение: 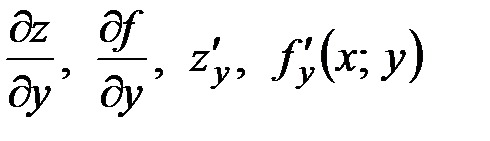 .
.
Частные производные вычисляются по формулам и правилам дифференцирования функции одной переменной, при этом все независимые переменные, кроме той, по которой ведется дифференцирование, следует считать постоянными. Однако переменные считаются константами только в процессе дифференцирования, а сами частные производные также являются функциями нескольких переменных.
Пример. Вычислить частные производные функций: 1) 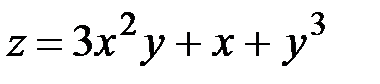 ; 2)
; 2) 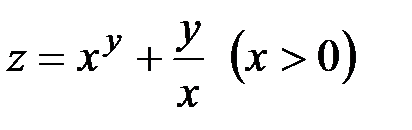 .
.
 1) При вычислении
1) При вычислении 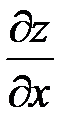 считаем
считаем 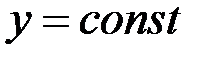 :
: 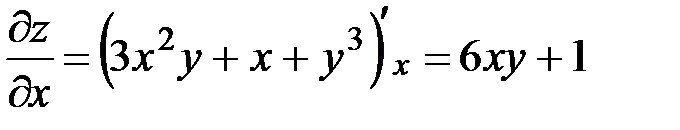 , при вычислении
, при вычислении 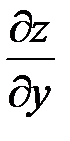 считаем
считаем 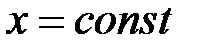 :
: 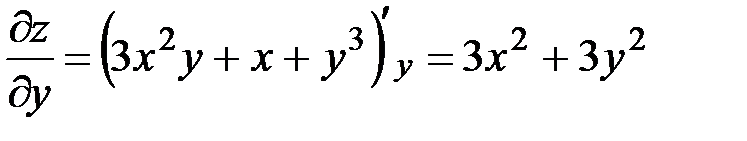 .
.
2) При вычислении 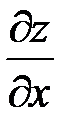 считаем
считаем 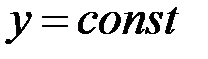 :
: 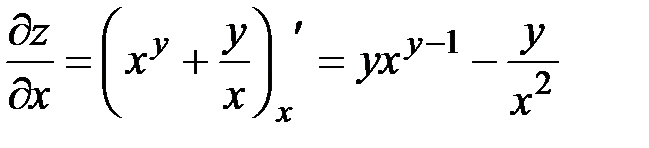 , при вычислении
, при вычислении 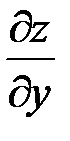 считаем
считаем 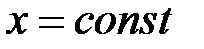 :
: 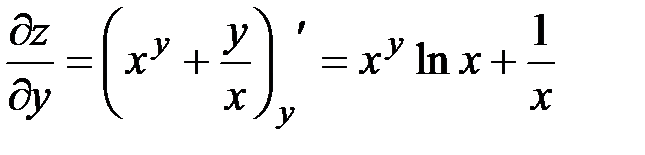 .
. 
Абсолютная величина частной производной 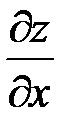 или
или 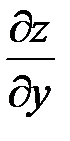 дает величину скорости, с которой происходит изменение функции
дает величину скорости, с которой происходит изменение функции 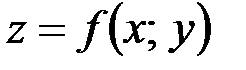 при изменении только
при изменении только 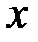 или только
или только 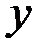 , а знак частной производной
, а знак частной производной 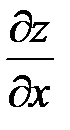 или
или 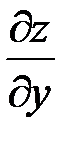 указывает на характер этого изменения (возрастание или убывание).
указывает на характер этого изменения (возрастание или убывание).
Аналогично определяются частные производные от функций любого числа независимых переменных. Пусть 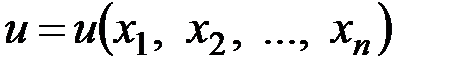 – функция
– функция 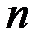 независимых переменных величин
независимых переменных величин 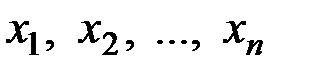 , тогда частная производная функции
, тогда частная производная функции 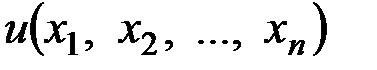 по переменной
по переменной 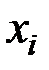 находится по формуле:
находится по формуле:
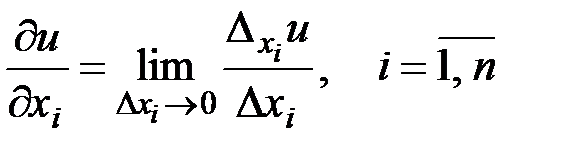 .
.
Частные дифференциалы и полный дифференциал
функций нескольких переменных.
Дифференцируемость функций нескольких переменных
Опр. Частным дифференциалом по 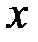 функции
функции 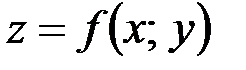 называется главная часть частного приращения
называется главная часть частного приращения 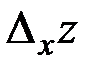 , пропорциональная приращению
, пропорциональная приращению 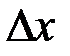 независимой переменной
независимой переменной 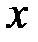 :
: 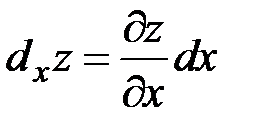 .
.
Аналогично: 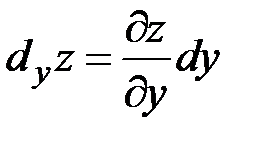 . Таким образом, частный дифференциал функции двух переменных равен произведению соответствующей частной производной на дифференциал этой переменной.
. Таким образом, частный дифференциал функции двух переменных равен произведению соответствующей частной производной на дифференциал этой переменной.
Для функции нескольких независимых переменных ее частный дифференциал по какой-нибудь из переменных равен произведению соответствующей частной производной на дифференциал этой переменной. Если 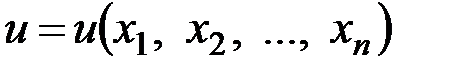 – функция
– функция 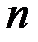 независимых переменных величин
независимых переменных величин 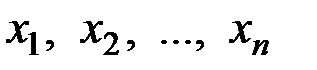 , тогда ее частный дифференциал по переменной
, тогда ее частный дифференциал по переменной 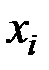 находится по формуле:
находится по формуле: 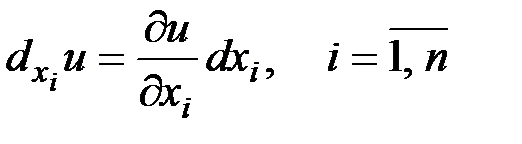 .
.
Пусть функция 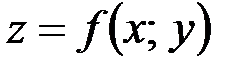 определена в окрестности точки
определена в окрестности точки 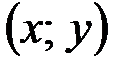 .
.
Опр. Функция 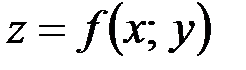 называется дифференцируемой в точке
называется дифференцируемой в точке 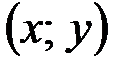 , если ее полное приращение в этой точке можно представить в виде:
, если ее полное приращение в этой точке можно представить в виде:
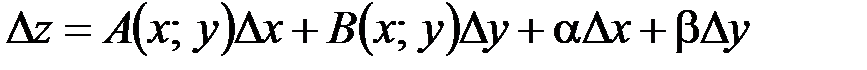 ,
,
где 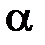 и
и 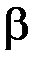 – бесконечно малые функции при
– бесконечно малые функции при 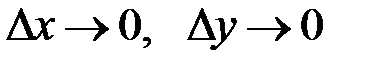 .
.
При этом слагаемое 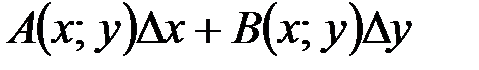 , линейное относительно
, линейное относительно 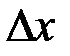 и
и 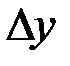 , называется главной частью приращения функции.
, называется главной частью приращения функции.
Теоремы (необходимые условия дифференцируемости).
Т1. Если функция 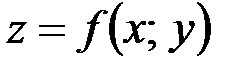 , определенная в окрестности точки
, определенная в окрестности точки 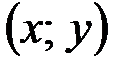 , дифференцируема в точке
, дифференцируема в точке 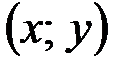 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Т2. Если функция 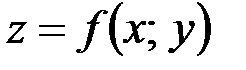 , определенная в окрестности точки
, определенная в окрестности точки 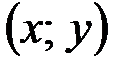 , дифференцируема в точке
, дифференцируема в точке 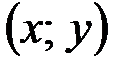 , то она имеет в этой точке частные производные
, то она имеет в этой точке частные производные 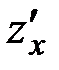 и
и 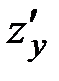 .
.
На основании Т2 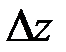 можно представить в виде:
можно представить в виде:
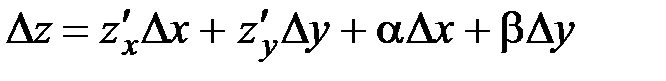 .
.
Теорема (достаточное условие дифференцируемости). Если в некоторой окрестности точки 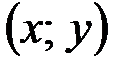 существуют частные производные
существуют частные производные 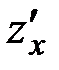 и
и 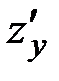 функции
функции 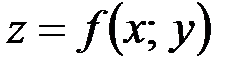 и они непрерывны в самой точке
и они непрерывны в самой точке 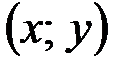 , то функция
, то функция 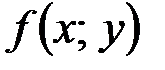 дифференцируема в этой точке.
дифференцируема в этой точке.
Опр. Полным дифференциалом функции 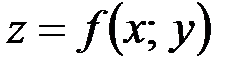 называется главная часть полного приращения
называется главная часть полного приращения 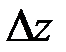 , линейная относительно приращений аргументов
, линейная относительно приращений аргументов 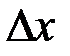 и
и 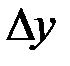 , т.е.
, т.е. 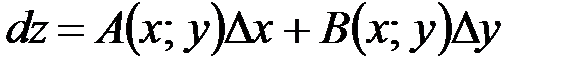 или
или 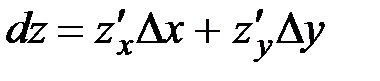 .
.
Если 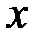 и
и 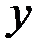 независимые переменные, то
независимые переменные, то 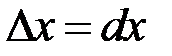 ,
, 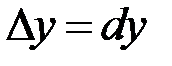 , и выражение для полного дифференциала окончательно примет вид:
, и выражение для полного дифференциала окончательно примет вид: 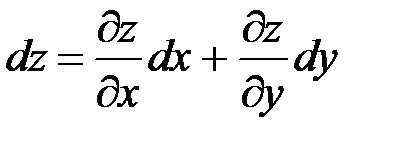 .
.
Последняя форма записи полного дифференциала сохраняет свой вид и в том случае, когда 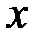 и
и 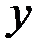 – зависимые переменные. Это свойство называется инвариантностью формы полного дифференциала.
– зависимые переменные. Это свойство называется инвариантностью формы полного дифференциала.
Нетрудно видеть, что полный дифференциал функции двух переменных равен сумме ее частных дифференциалов: 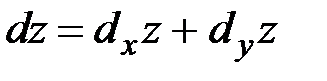 .
.
Полный дифференциал функции 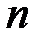 независимых переменных
независимых переменных 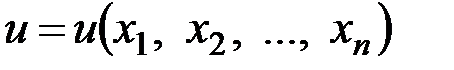 равен сумме произведений соответствующих частных производных на дифференциалы этих переменных:
равен сумме произведений соответствующих частных производных на дифференциалы этих переменных: 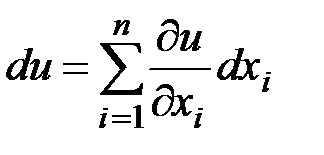 .
.
 2015-02-24
2015-02-24 2595
2595
