В течение семестра студенты решают задачи, указанные преподавателем, к каждому практическому занятию. Проводится 3 аудиторные контрольные работы.
Студент допускается до экзамена после получения зачета по контрольным работам и выполнения индивидуальных заданий преподавателя в рамках отведенного времени (9 часов самостоятельной работы).
Примеры задач для контрольных работ приведены ниже.
Итоговый контроль по дисциплине «Линейная алгебра» предлагается проводить в форме устного экзамена по билетам. Каждый билет состоит из 7 вопросов: 1 теоретический вопрос и 6 задач тестового уровня. Каждый вопрос относится к одному из семи разделов дисциплины. Ответ на теоретический вопрос оценивается в 0,5-2 балла, каждая решенная задача оценивается в 0,5 балла. Таким образом:
· оценка «отлично» выставляется студенту, набравшему 4,5-5 баллов;
· оценка «хорошо» выставляется студенту, набравшему 4 балла;
· оценка «удовлетворительно» выставляется студенту, набравшему 3,5 балла;
· оценка «неудовлетворительно» выставляется студенту, набравшему менее 3,5 баллов.
Примерный вариант контрольной работы 1
Даны матрицы 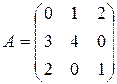 и и 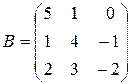 . .
| Найти матрицы 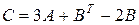  . .
| ||
Даны матрицы 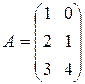 и и 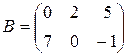 .
Найти матрицы .
Найти матрицы 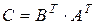 и и  . .
| |||
| Два однотипных, но различных по качеству продукта продаются в трех магазинах. Матрица А – объемы продаж этих продуктов в 1-м квартале, матрица В – во 2-м квартале (в тыс. руб.). Определить: 1) объемы продаж каждого продукта за два квартала по каждому магазину; 2) объемы продаж каждого продукта за два квартала во всех магазинах; 3) общий объем продаж за два квартала; |
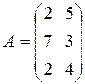 , , 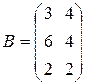
| ||
Найти миноры и алгебраические дополнения элементов 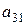 и и 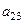 матрицы матрицы
| 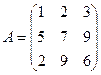
| ||
Вычислить определитель 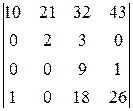 . .
| |
Найти матрицу, обратную к матрице 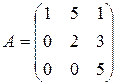 двумя способами:
методом присоединенной матрицы и методом Гаусса. двумя способами:
методом присоединенной матрицы и методом Гаусса.
| |
Найти ранг матрицы 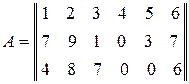 , указать какой-либо базисный минор. , указать какой-либо базисный минор.
| |
Являются ли строки: 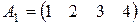 , , 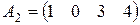 и и 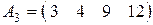 линейно независимыми линейно независимыми
|
Примерный вариант контрольной работы 2
Точка В симметрична точке А относительно координатной плоскости yOz.
Точка С – проекция точки А на координатную ось Oх.
Найти координаты точек В и С, если 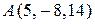 . Построить чертеж. . Построить чертеж.
| |
Найти координаты вектора 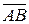 , если , если 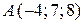 и и 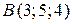
| |
Найти проекции вектора 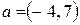 на оси координат на оси координат
| |
Найти длину вектора 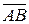 , если , если 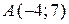 , , 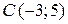 , ,  ,
а точка ,
а точка 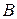 делит отрезок делит отрезок 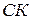 пополам. пополам.
| |
Найти координаты вектора 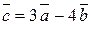 , если , если 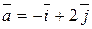 и и 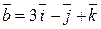 . .
| |
В треугольнике АВС сторона АВ разделена точкой М в отношении 1:4, считая от точки А. Найти разложение вектора 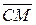 по векторам по векторам 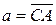 и и 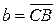
| |
Найти скалярное произведение векторов 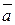 и и 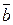 , если , если 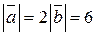 , угол между векторами равен 120 градусам. , угол между векторами равен 120 градусам.
| |
Найти величину 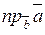 , если , если 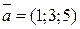 и и 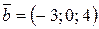 . .
| |
Найти направляющие косинусы вектора 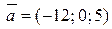
|
Найти угол между векторами 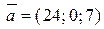 и и 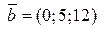
| |
Найти векторное произведение векторов 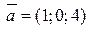 и и 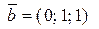
| |
Найти угол между векторами 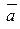 и и 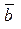 , если , если 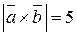 , , 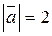 , , 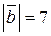 . .
| |
Найти смешанное произведение векторов 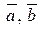 и и 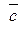 , если , если
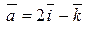 ; ; 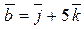 ; ; 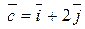 . .
| |
Найти значение параметра 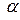 , при котором векторы , при котором векторы 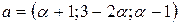 и и 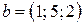 ортогональны. ортогональны.
| |
Найти значение параметра 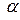 , при котором векторы , при котором векторы 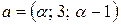 , , 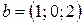 и и 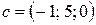 компланарны. компланарны.
| |
Образуют ли базис в пространстве векторы 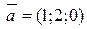 , , 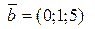 и и 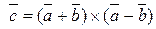 ? Почему? ? Почему?
| |
Укажите какой-либо вектор 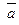 , который с векторами , который с векторами  и и 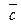 образует базис в пространстве: образует базис в пространстве: 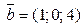 и и 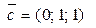
|
Примерный вариант контрольной работы 3
| Составить каноническое уравнение прямой, проходящей через точки А(1; 5) и В(-2; 0). Записать параметрическое уравнение этой прямой, общее уравнение прямой. Указать направляющий и нормальный векторы этой прямой. | |
Найти угол между прямыми 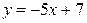 и и 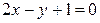
| |
Указать направляющий вектор 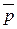 прямой прямой 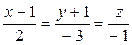 .
Составить уравнение плоскости, перпендикулярной данной прямой. .
Составить уравнение плоскости, перпендикулярной данной прямой.
| |
Найти расстояние от точки 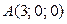 до плоскости до плоскости 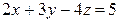 . .
| |
Составить уравнение прямой, перпендикулярной плоскости 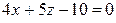 . .
| |
Определить координаты фокусов 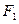 и и 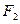 эллипса эллипса 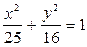 . Сделать чертеж. . Сделать чертеж.
| |
| Выполнить схематический чертеж однополюсного гиперболоида. | |
Решить методом обратной матрицы, методом Крамера и методом Гаусса СЛУ 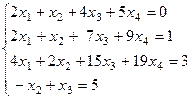
|
Совместна ли СЛУ, заданная расширенной матрицей системы
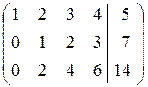 ? ?
| |
Является ли  общим решением ОСЛУ общим решением ОСЛУ 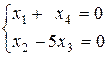 ? ?
| |
| Доказать, что векторы (1;1;3), (-3;2;1), (1;2;4) линейно независимы, т.е. образуют базис, и найти координаты вектора (1;2;3) в этом базисе. | |
При каком значении k 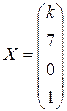 является частным решением СЛУ является частным решением СЛУ 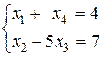 ? ?
|
 2015-03-20
2015-03-20 196
196








