Механические колебания и волны

3.1.4.1. Движение в центральном поле сил.

Квантовая механика занимает своеобразное положение в ряду физических теорий. Обычно более общая теория может быть сформулирована логически замкнутым образом, не зависимо от менее общей теории, являющейся её предельным случаем. Так, релятивистская механика может быть построена на основании своих принципов, без всяких ссылок на ньютоновскую механику. Формулировка же основных положений квантовой механики, принципиально невозможна без привлечения механики классической. Таким образом, квантовая механика содержит в себе классическую в качестве своего предельного случая. Мало того, она нуждается в этом самом предельном случае для самого своего обоснования. При этом переход от классической механики к квантовой, осуществляется через механику колебаний и волн по-аналогии с тем, как происходит предельный переход от волновой к геометрической оптике. Необходимо подчеркнуть, что указанный выше предельный переход не только неизбежен, но и необходим. Он позволяет представить квантовую механику не как систему постулатов «загадочного» происхождения, а как стройную физическую теорию с определённым логическим выводом (терминологически и идейно) из классического подхода. Так, при выводе уравнения Шрёдингера, достаточно удобным является рассмотрение движения частицы в центральном поле сил. Характерными примерами систем такого типа является гармонический осциллятор и движение частицы в кулоновском поле сил. Говорят, что задано центральное поле сил, если потенциальная энергия U зависит только от расстояний между частицами. Для одной частицы это предполагает зависимость U только от длины 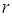радиус-вектора :

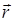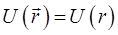
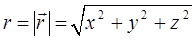
О потенциальном поле 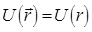в общем случае говорят как о поле сферической симметрии. Наличие такой симметрии приводит в общем случае к дополнительным интегралам движения. Покажем, что одним из них является вектор момента импульса (углового момента) :

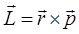
почленное дифференцирование данного выражения даёт:

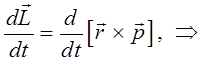
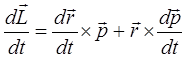
однако в силу того, что:

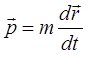
первый член в выражении:

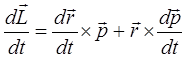
исчезает как векторное произведение коллинеарных векторов, т.е.

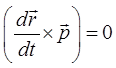
Во втором члене следует иметь ввиду уравнения движения:

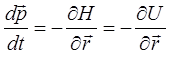
При вычислении компонент градиента:

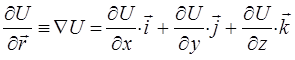
учтём сферическую симметрию:

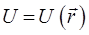
т тогда непосредственно из выражения вида:

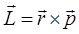
находим:

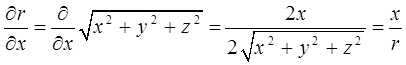
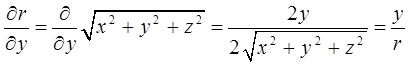
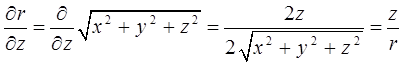
а также учитывая, что:

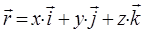
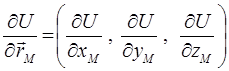
получаем, что сила направлена по радиус-вектору:

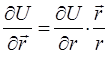
Следовательно, вектор 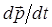в выражении:

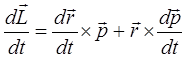
коллинеарен 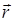, т.е.

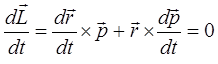
и таким образом:

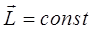
Закон сохранения импульса (углового момента) имеет наглядную геометрическую интерпретацию. Так, поскольку пары векторов:

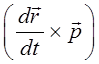и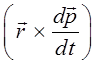

являются коллинеарными, то это в свою очередь означает, что движение частицы будет происходить в одной фиксированной плоскости, перпендикулярной постоянному вектору .Это утверждение следует из смысла векторного произведения и интерпретации 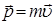как вектора, касательного траектории движения. По этой причине можно говорить, что в центральном поле сил орбитальное движение является в общем случае плоским.

3.1.4.1.а. Гармонический осциллятор.

Рассмотрим простейший тип колебательного движения – свободные (собственные) незатухающие механические колебания, т.е. такие колебания, которые совершаются без внешнего воздействия за счёт первоначально полученной телом энергии. При рассмотрении колебаний такого вида – пренебрегают силой сопротивления. Простейшим типом колебательного движения являются гармонические колебания, т.е. такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Рассмотрим одномерное движение частицы (материальной точки) с массой 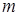, на которую действует вдоль одной из координатных осей упругая возвращающая сила 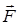. Очевидно, при малых отклонениях частицы (материальной точки) от положения равновесия, под действием упругой возвращающей силы 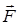, будут совершаться колебания относительно этой точки равновесия. Такую колебательную систему называют гармоническим осциллятором. Примерами гармонического осциллятора являются пружинный (материальная точка на пружине), математический и физический маятники, а также колебательный контур (для токов и напряжений столь малых, что элементы контура можно было бы считать линейными). Пусть у нас имеется некоторое тело массой – m, материальная точка, подвешенное на пружине жёсткостью 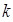. В этом положении упругая сила 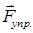, приложенная к телу, уравновешивает силу тяжести 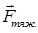, т.е. в данном случае справедливо равенство:

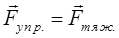
Тогда смещение материальной точки относительно оси 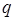, положение равновесия, очевидно будет равно нулю, т.е. 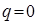. Если к телу приложить некоторую силу 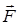, оттянув пружину, т.е. сместив данное тело из положения равновесия, при котором 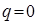, то тело выйдет из состояния равновесия. При этом на тело будет действовать большая упругая сила 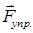, которая будет тем больше, чем большее смещение будет получать подвешенное на пружине тело.

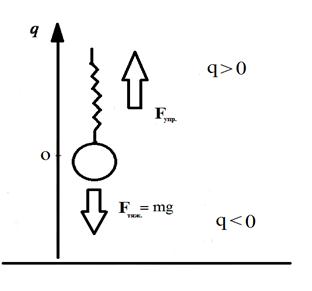
Рис. 1. Модель гармонического осциллятора

Очевидно для рассматриваемой системы гармонического осциллятора, будут справедливы условия вида:

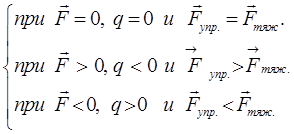
Согласно закону Гука, при упругих деформациях возникает сила, направленная к положению равновесия и пропорциональная смещению тела (его деформации), т.е.

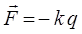
здесь 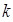– коэффициент пропорциональности (жёсткость пружины). Знак минус в данном выражении показывает, что возвращающая сила 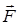всегда направлена в сторону положения равновесия. Силы, неупругие по природе, но аналогичные по свойствам, называют квазиупругими. Квазиупругие силы обычно возникают при малых деформациях. Таким образом, изменение упругой силы, пропорционально изменению длины пружины или смещению тела. На основании выражения второго закона Ньютона:

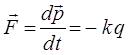
а также учитывая, что:

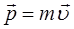
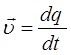
откуда:

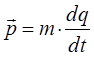
после соответствующих подстановок, получим дифференциальное уравнение, описывающее одномерное движение материальной точки:

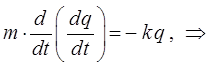
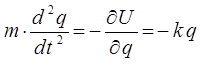
преобразуя полученное выражение к виду:

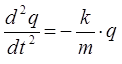
принимая:

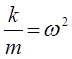
будем иметь соответственно:

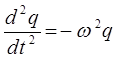
откуда соответственно:

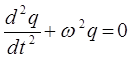
К аналогичному уравнению можно прийти и несколько другим путём, используя формальные подходы Лагранжа и Гамильтона, рассмотренные нами уже ранее. Так, при рассмотрении задачи на гармонический осциллятор, выражение для функции Лагранжа, в рамках соответствующего подхода, очевидно, будет иметь вид:

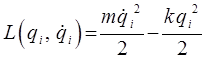
здесь обобщённая координата 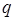, есть величина отклонения частицы с массой 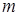от положения равновесия, а 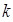– константа жёсткости. Найдём теперь обобщённый импульс 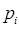и обобщённую силу 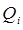, имеем соответственно:

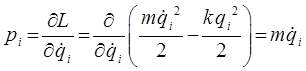
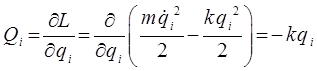
и подставим полученные выражения для обобщённой силы 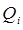и обобщённого импульса 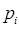в уравнение Лагранжа:

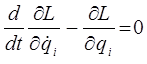
учитывая, что:

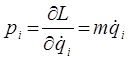
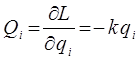
имеем:

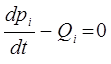
откуда соответственно:

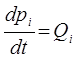
или после соответствующих подстановок:

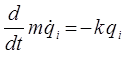
Учитывая, что:

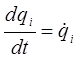
имеем:

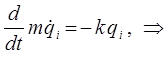
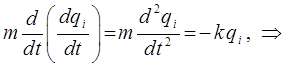
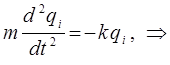
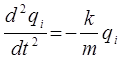
принимая:

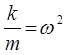
имеем:

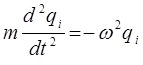
или

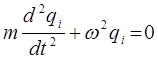
Аналогичным образом решается такого рода задача и в формализме Гамильтона. Для этих целей представим полную энергию рассматриваемой системы как сумму кинетической и потенциальной энергий, т.е.

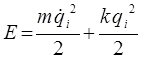
или в импульсной форме:

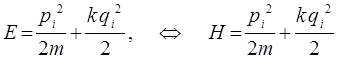
Учитывая уравнения Гамильтона:

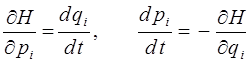
или

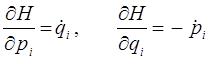
исходя из уравнения вида:

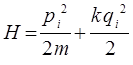
имеем соответственно:

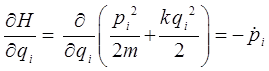
и таким образом:

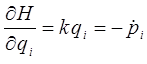
а также:

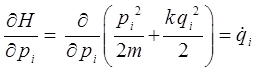
откуда:

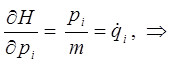
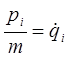
или

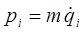
Подстановка полученного выражения для обобщённого импульса 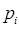в уравнение:

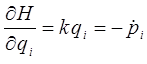
приводит к уравнению Ньютона:

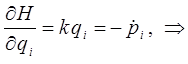
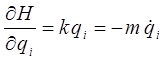
или

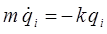
Учитывая, что:

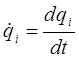
имеем:

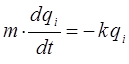
откуда:

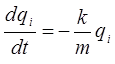
принимая:

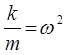
имеем:

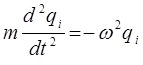
или

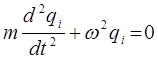
Таким образом, решение задачи о гармоническом осцилляторе в рамках формализма Гамильтона, как и в случае формализма Лагранжа, совпадает с результатами механики Ньютона. Полученное выражение представляет собой линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. В общем случае, линейным дифференциальным уравнением второго порядка называется уравнение первой степени, линейное относительно

неизвестной функции и её производных. Будем записывать его в виде:

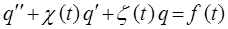
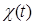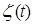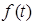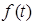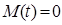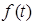где и – постоянные. Функция называется правой частью уравнения. Если функция тождественно равна нулю (как в нашем случае), то такое уравнение называется линейным уравнением без правой части (или однородным). В противном случае – линейным уравнением с правой частью (или неоднородным). Достаточно очевидно, что при и , дифференциальное уравнение:

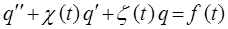
сводится к уравнению вида:

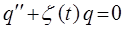
в данном уравнении:

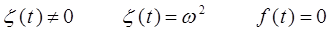
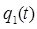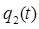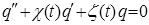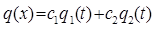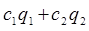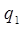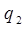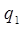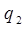Теорема 1: «Если и – решения линейного уравнения , то функция вида при любых постоянных c₁ и c₂ , также является решением уравнения. Здесь выражение является линейной комбинацией соответствующих частных решений и ». Из сказанного выше можно заключить, что если и – решения уравнения:

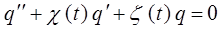
такие, что их отношение не равно постоянной величине:

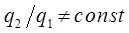
то линейная комбинация этих функций 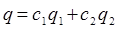, является решением дифференциального уравнения. Нахождение общего решения дифференциального уравнения принципиально, т.к. из общего решения при любых заданных условиях может быть найдено частное решение, удовлетворяющее этим условиям. Для проверки линейной независимости функци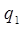й и 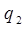, являющихся частными решениями дифференциального уравнения, необходимо составить и решить так называемый определитель Вронского (Вронскиан) 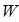. При этом Вронскиан не должен обращаться в нуль :

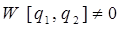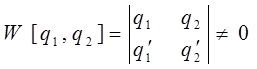
Обычно частные решения дифференциального уравнения ищут в виде показательной функции 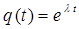, где 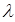- постоянная величина. Такой выбор вида частного решения обусловлен тем, что это единственная элементарная функция, все производные которой подобны между собой и к самой функции. Функцию вида 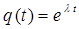называют ещё стандартной подстановкой. Дифференцируя функцию 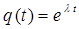, беря вначале первую, а затем вторую производную:

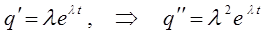
Возвратимся теперь к исходному дифференциальному уравнению:

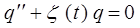
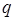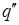очевидно подстановка значения и в данное уравнение, даст выражение вида:

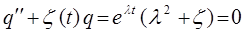
Поскольку 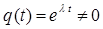, то из последнего уравнения следует, что:

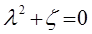
такое уравнение относительно 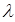, называется характеристическим уравнением, отвечающим соответствующему дифференциальному уравнению:

,

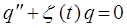а функция 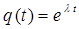является стандартной подстановкой (частным решением дифференциального уравнения), с помощью, которой решается исходное дифференциальное уравнение. При этом, 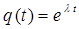будет частным решением соответствующего уравнения лишь в том случае, если 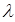- корень характеристического уравнения. Таким образом, для решения искомого дифференциального уравнения необходимо составить и решить характеристическое уравнение. Чтобы составить характеристическое уравнение, нужно в данном дифференциальном уравнении 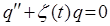заменить 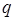единицей, а производную искомой функции 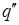– величиной 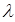в степени, равной порядку производной 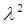соответственно. При этом следует различать следующие три возможные случая для корне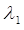й и 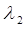характеристического уравнения (предполагается, что коэффициенты M и N – действительные числа):

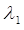· и 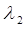– корни уравнения действительные и различные числа, т.е. .

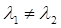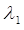· и 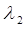– корни уравнения действительные и равные числа, т.е. .

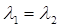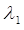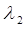· и – корни уравнения комплексные сопряжённые числа: 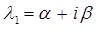и

.

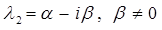Учитывая, что:

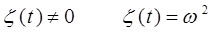
представим уравнение:

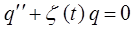
к виду:

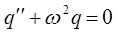
Запишем теперь, в соответствии с правилами указанными выше, характеристическое уравнение:

,

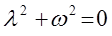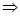
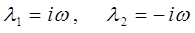
имеем соответственно два независимых решения искомого дифференциального уравнения. Таким образом, решив характеристическое уравнение, мы приходим к выводу о том, что корни уравнения – комплексно сопряжённые числа (третий из выше перечисленных случаев). В соответствии с приведенной выше теоремой об общем решении дифференциального уравнения, в независимости от того являются ли корни характеристического уравнения действительными или комплексными сопряжёнными числами, общее решение имеет вид

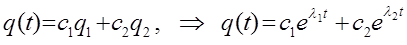
Поскольку в нашем случае, корни характеристического уравнения являются комплексными сопряжёнными числами, т.е. имеет место два независимых решения:

общее решение можно записать в виде:

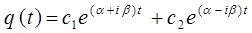
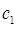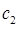здесь и – произвольные комплексные постоянные. Учитывая, что:

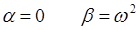
тогда на основании выше приведенных выкладок можно заключить, что:

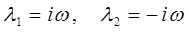
Учитывая, что общее решение дифференциального уравнения строится как суперпозиция частных решений:

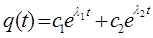
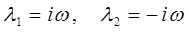
будем иметь соответственно:

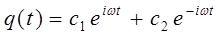
здесь частными являются решения вида:

на основании известных из курса линейной алгебры формул Эйлера:

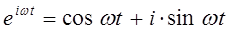
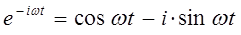
откуда следует, что:

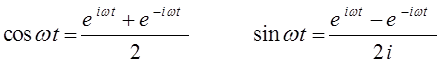
а также принимая, что:

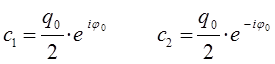
получим соответственно уравнение вида:

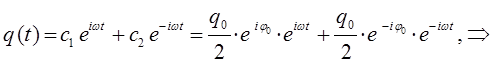
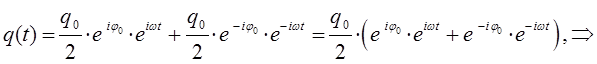
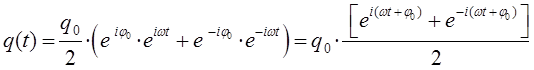
поскольку по определению:

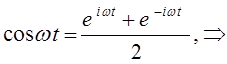
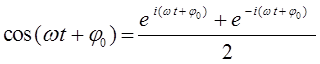
тогда выражение вида:

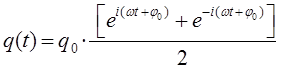
очевидно, может быть представлено к виду:

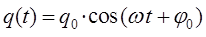
Если же принять, что:

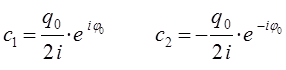
тогда будем иметь соответственно:

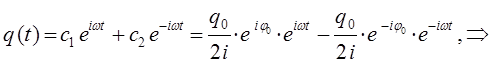
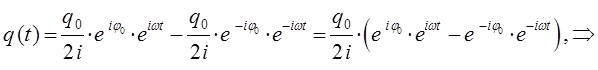
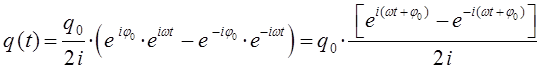
поскольку:

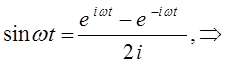
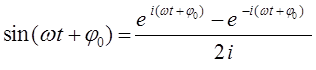
тогда выражение:

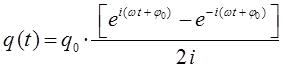
очевидно, может быть представлено к виду:

Таким образом, путём соответствующих преобразований, на основании общего решения дифференциального уравнения:

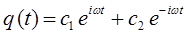
мы пришли к двум эквивалентным друг другу решениям дифференциального уравнения, записанным в тригонометрической формах:

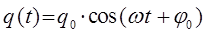
К аналогичному результату можно прийти и несколько другим путём. В соответствии с приведенной выше теоремой об общем решении, в независимости от того являются ли корни характеристического уравнения действительными или комплексными сопряжёнными числами, общее решение дифференциального уравнения строится в виде:

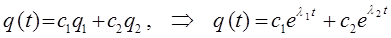
Поскольку в нашем случае, корни характеристического уравнения являются комплексными сопряжёнными числами, т.е. имеет место два независимых решения:

тогда общее решение можно записать в виде:

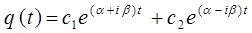
здесь с₁ и с₂ –произвольные комплексные постоянные. Учитывая, что:

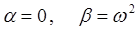
заключаем, что:

тогда общее решение можно представить к виду:

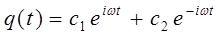
где выражения:

есть частные решения дифференциального уравнения. Очевидно:

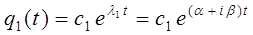
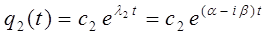
тогда на основании формул Эйлера:

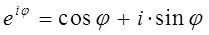
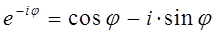
будем иметь соответственно:

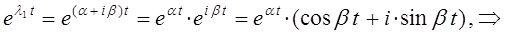
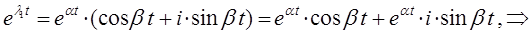
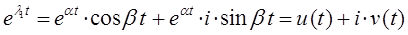
и аналогично:

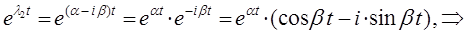
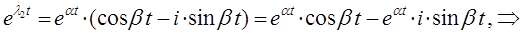
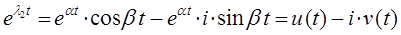
В общем случае, если дифференциальное уравнение вида:

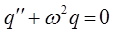
имеет комплексные сопряжённые решения вида:

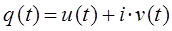
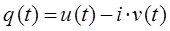
то каждая из функци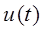й и 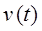, вне зависимости от того какое из частных решений мы используем для построения общего решения в действительной (вещественной) форме, будет являться решением этого уравнения. Учитывая форму общего решения уравнений такого типа:

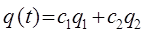
а также частные решения вида (при и ):

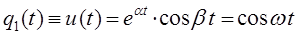
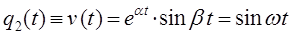
строим общее решение дифференциального уравнения в виде:

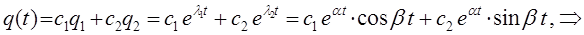
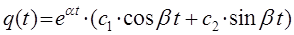
поскольку 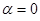и 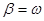, имеем соответственно:

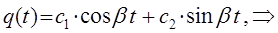
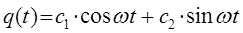
Вводя вспомогательный угол 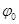, имеем:

очевидно, при этом должно соблюдаться условие вида:

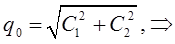
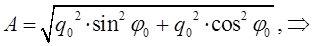
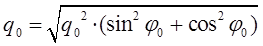
учитывая при этом, что:

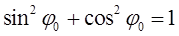
будем иметь соответственно:

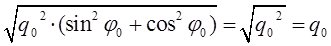
Очевидно также и другое:

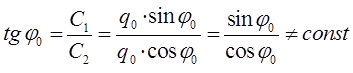
поэтому соответственно:

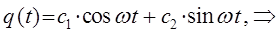
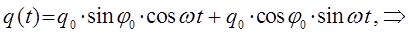
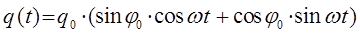
поскольку:

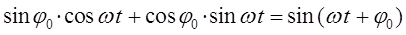
поэтому:

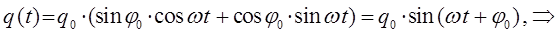
Поскольку в результате решения дифференциального уравнения мы получаем суперпозицию решений:

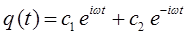
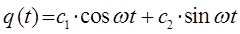
то будет верно и другое:

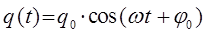
Данное утверждение легко проверить, вводя вместо соответствующих коэффициентов 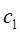и 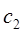вспомогательный угол 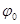, т.е.

тогда соответственно:

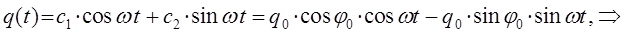
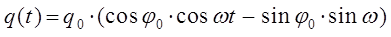
учитывая, что:

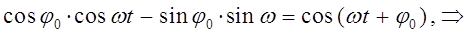
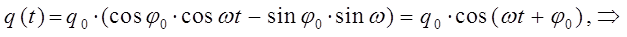
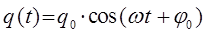
Таким образом, путём соответствующих преобразований мы пришли к двум эквивалентным друг другу решениям дифференциального уравнения, записанным в показательной и тригонометрической формах.

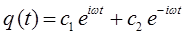
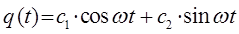
из которых следуют уравнения вида:

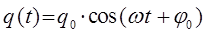
Нетрудно заметить, что:

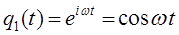
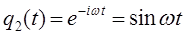
здесь величина 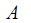есть амплитуда колебания, характеризующая размах колебательного движения, величину смещения материальной точки от положения равновесия. Аргумент 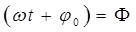называется фазой колебания, а 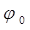– начальной фазой колебания в момент времени 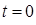. Достаточно очевидно, что:

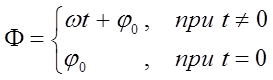
Расстояние, отделяющее колеблющуюся точку от положения равновесия, характеризует величина 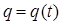. В общем случае амплитуда и начальная фаза колебания определяются начальными условиями движения, т.е. положением и скоростью материальной точки в момент времени 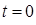. Среди различных видов колебательного движения, гармонические колебания являются наиболее простыми. Необходимо отметить, что поскольку величина 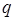характеризует смещение материальной точки от положения равновесия, а величина 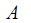- амплитуду колебательного движения (размах колебания), тогда при условии:

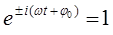
величина 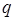будет сводиться к величине, 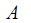и будет характеризовать, таким образом, максимальное отклонение колеблющейся материальной точки от положения равновесия, т.е. будет справедливо уравнение вида:

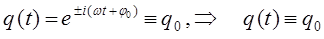
Необходимо также отметить, что при преобразовании дифференциального уравнения, описывающего колебания гармонического осциллятора, величина 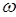была введена чисто формально, в то время как она имеет глубокий физический смысл, определяя частоту колебаний. Величина 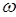называется круговой (циклической) частотой. Выведенное для гармонического осциллятора дифференциальное уравнение, показывает, что данная величина зависит от жёсткости пружины и массы материальной точки. Аналогичная угловой скорости 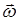, она связывает линейную скорость и период колебаний, представляя, таким образом, число периодов колебаний, за которые фаза колебания получит приращение 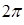. Это становится очевидным из следующих рассуждений. Поскольку формально:

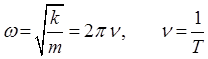
тогда соответственно:

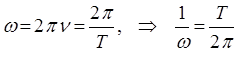
и таким образом:

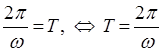
Очевидно, чем больше по величине будет круговая (циклическая) частота, тем меньше будет величина периода колебательного движения. Проводя аналогию между угловой скоростью и циклической частотой, можно увидеть, что чем больше будет скорость, с которой колеблющаяся точка совершит полный оборот на 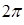при своём движении, получая, таким образом, приращение , тем за меньшее время будет совершено системой колебательное движение. Таким образом, частица около точки равновесия совершает гармоническое (по закону синуса или косинуса) колебательное движение с циклической частотой 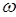. В связи с этим колебательные системы такого типа называют гармоническим осциллятором. Как известно, в центральном поле сил, потенциальная энергия частицы (системы частиц) зависит от расстояния между частицей (системой частиц) и центром силового поля. Обычно для наглядности, задачу о движении в центральном поле сил сводят к двум моделям – модели гармонического осциллятора и движении частицы в кулоновском поле сил. Как известно, гармонический осциллятор представляет собой колебательную систему, которая совершает свободные (собственные) незатухающие механические колебания, совершаемые без внешнего воздействия за счёт первоначально полученной телом энергии. При рассмотрении колебаний такого вида – пренебрегают силой сопротивления, а совершающиеся непрерывные осциллирующие движения рассматривают как гармонические, т.е. как такие, что совершаются в системе по закону синуса или косинуса. Такие непрерывные колебательные движения, очевидно, могут осуществляться только под действием квазиупругой силы, т.е. такой, что возникает в системе при малых деформациях. Поскольку, в случае гармонического осциллятора, колебательное движение будет совершаться под действием упругой возвращающей силы, то при малых деформациях частица (система частиц) в данном случае, будет совершать колебания относительно положения равновесия. Поскольку квазиупругая сила является консервативной по своей природе, поэтому полная энергия такой системы должна оставаться постоянной. Действительно, пусть общее решение дифференциального уравнения, описывающего колебания гармонического осциллятора имеет вид:

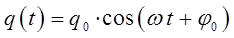
Cогласно закона Гука, сила упругости пропорциональна деформации:

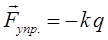
на основании третьего закона Ньютона, для преодоления силы упругости пружины, необходимо приложить силу 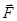, равную:

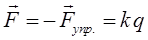
Очевидно элементарная работа 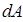, совершаемая силой 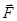при малых деформациях, будет определяться выражением вида:

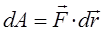
учитывая, что 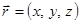и работа смещения осуществляется вдоль одной из координатных осей, имеем:

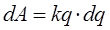
откуда:

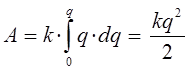
Запишем выражение для полной энергии гармонического осциллятора:

потенциальная энергия осциллятора имеет параболическую зависимость от координаты т.е.

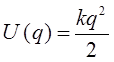
что, очевидно, соответствует закону Гука:

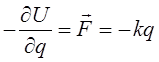
выражение для кинетической энергии осциллятора:

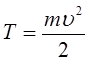
с учётом выражений:

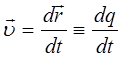
можно представить к виду:

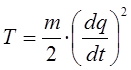
тогда выражение для полной энергии гармонического осциллятора:

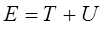
может быть задано уравнением вида:

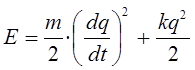
или, что то же самое:

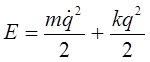
Учитывая общее решение дифференциального уравнения, описывающего колебания гармонического осциллятора:

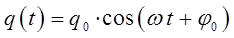
будем иметь для общей энергии колебательной системы выражение вида:

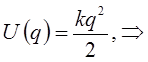
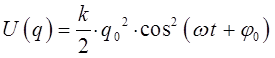
поскольку:

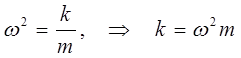
тогда после подстановки получаем соответственно:

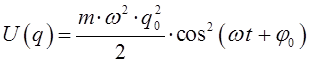
аналогично, для кинетической энергии имеем:

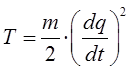
откуда соответственно:

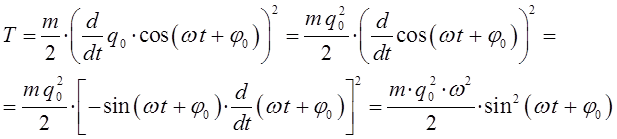
Таким образом, для потенциальной и кинетической энергий, приходим соответственно к выражениям вида:

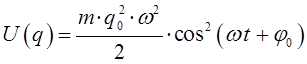
и соответственно:

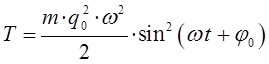
после их подстановки в выражение для полной энергии осциллятора:

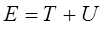
будем иметь:

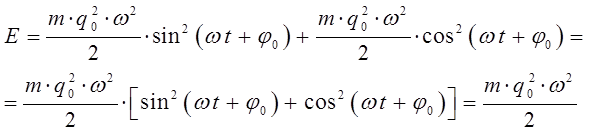
Итак, имеем для полной энергии осциллятора выражение вида:

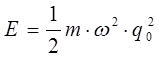
Таким образом, в процессе колебательного движения происходит превращение кинетической энергии в потенциальную и обратно, причём в моменты наибольшего отклонения от положения равновесия, полная энергия системы будет состоять, только из потенциальной энергии, которая будет достигать своего наибольшего значения 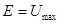. Точки, в которых потенциальная энергия равна полной энергии 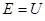, называют точками остановки. В точках остановки (поворота) кинетическая энергия обращается в нуль. Если движение материальной точки происходит между двумя точками остановки, его называют финитным. Если же движение не ограничено или ограничено только одной точкой остановки, то его называют инфинитным. В соответствии с выше изложенным можно заключить, что гармонический осциллятор совершает одномерное финитное движение. Это означает, что частица совершает периодически повторяющиеся движения между двумя точками остановки. Такое движение называют колебательным. При финитном движении в точках остановки кинетическая энергия осциллятора обращается в нуль и полная его энергия равна его потенциальной энергии. В промежутках между двумя точками остановки, потенциальная энергия уменьшается и при прохождении через положение равновесия – обращается в нуль. В этом случае полная энергия системы будет равна его кинетической энергии.

3.1.4.1.б. Рассмотрение движения частицы в поле постоянного потенциала. Введение представлений о круговых орбитах.

Рассмотрим теперь движение частицы с зарядом 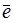в кулоновском поле, которое создаётся другой частицей с зарядом 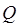. Поскольку движение такой частицы происходит в центральном силовом поле, то момент импульса частицы относительно центра масс сохраняется; т.е. имеем соответственно:

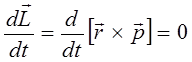
откуда:

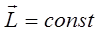
это утверждение легко доказать. Так, имеем соответственно:

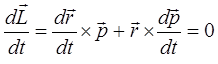
Так как пары векторов:

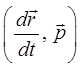и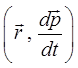

являются коллинеарными, то движение частицы будет происходить, очевидно, в одной плоскости, и орбита частицы, таким образом, будет являться плоской. Пусть движение частицы происходит в плоскости 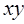. В этом случае две компоненты вектора момента импульса частицы 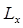и 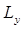очевидно будут равняться нулю. Тогда вектор момента импульса можно будет очевидно записать как:

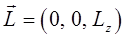
т.е. движение частицы будет совершаться в плоскости, перпендикулярной оси 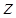. Таким образом, в силу закона сохранения момента импульса в центральном поле сил 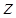- компонента момента импульса будет являться постоянной величиной:

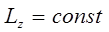
Обычно движение частицы в центральном поле сил удобно рассматривать в полярных координатах 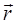и 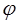. В целях дальнейших выкладок выясним, как будет выглядеть гамильтониан в полярной системе координат.

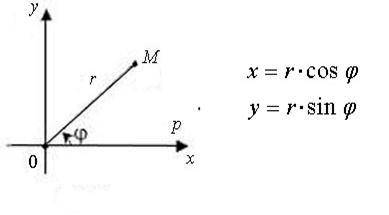
Рис.7.

Так, пусть задана частица, движущаяся в плоскости (x, y), при этом 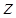очевидно будет равно нулю. Необходимо получить канонические уравнения движения в полярной системе координат. Для этого установим уравнения связи между линейными координатами частицы и её угловыми характеристикам. В общем случае полярная система координат представляет собой двумерную систему координат, в которой каждая точка плоскости определяется двумя числами – полярным углом 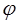и полярным радиусом 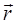. Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется в общем случае двумя полярными координатами – радиальной и угловой. Так, выражая гамильтониан в явном виде через обобщённые импульсы 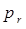и 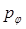, считая при этом, что у потенциала U эта замена уже проведена, будем иметь

соответственно выражение вида::

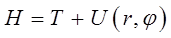
Учитывая, что:

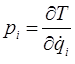
имеем соответственно:

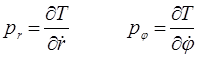
В рамках рассматриваемой задачи кинетическая энергия E, входящая в выражение для гамильтониана H, в декартовой системе координат:

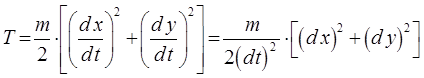
Сумма квадратов дифференциалов, может быть, очевидно, вычислена непосредственным дифференцированием выражений:

тогда:

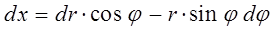
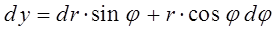
и соответственно:

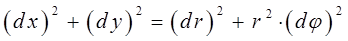
Следовательно, кинетическую энергию T можно рассматривать с этих позиций как некоторую функцию обобщённых скоростей , т.е. имеем соответственно:

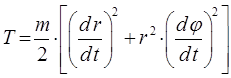
откуда находим радиальный 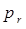и угловой 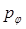импульсы:

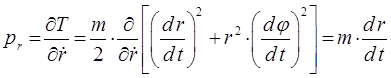
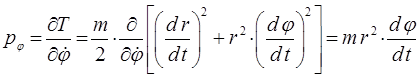
и таким образом:

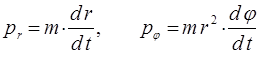
откуда:

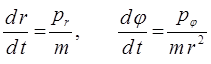
подставляя полученные выражения в уравнение:

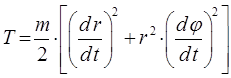
имеем соответственно:

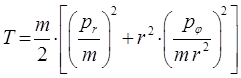
откуда:

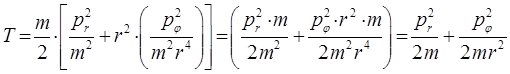
и таким образом:

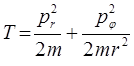
Подстановка аналитического выражения для кинетической энергии в уравнение:

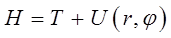
даёт искомое выражение гамильтониана в полярных координатах:

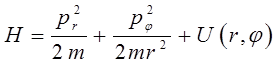
Выясним теперь вид гамильтониана в сферической системе координат. Сферическая система координат представляет собой трёхмерную систему координат:

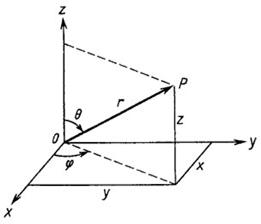
Рис.8.

В данной системе координат каждая точка пространства задаётся тремя числами – радиус-вектором 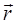, определяющим расстояние от начала координат до некоторой точки P и двумя углами – 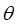, образующим угол между положительным направлением оси Oz и радиус-вектором точки P и 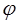– образованном проекцией радиус-вектора на плоскость Oxy с положительным направлением оси Ox. Используя формализм Гамильтона, рассмотрим задачу о построении функции Гамильтона (гамильтониана) для частицы в сферической системе координат. Итак, положение материальной точки P в сферической системе координат задаётся тремя величинами: радиус-вектором 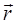, который характеризует расстояние от точки до центра координат и двумя углам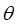и и 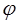. Взаимосвязь между этими тремя величинами и декартовой системой координат определяется соотношениями вида:

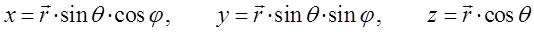
Компоненты вектора в декартовой системе координат могут быть выражены далее через соответствующие компоненты сферической системы координат:

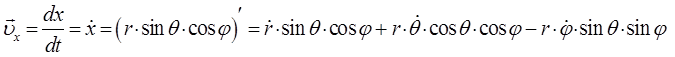
и аналогично для двух других компонент скорости будем иметь соответственно:

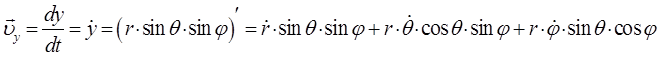
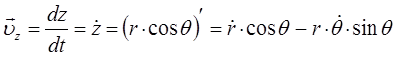
Запишем аналитическое выражение для функции Гамильтона в декартовой системе координат. При этом учтём, что кинетическая энергия частицы должна быть выражена через импульсы. Так, имеем соответственно:

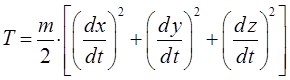
откуда соответственно:

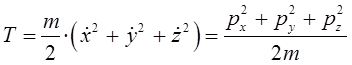
здесь:

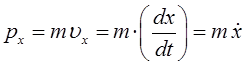
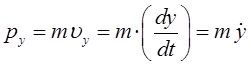
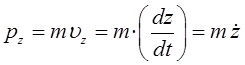
Таким образом, функцию Гамильтона можно представить к виду:

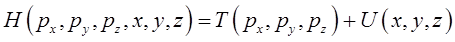
Учитывая, что:

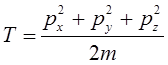
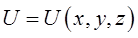
имеем:

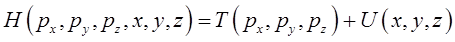
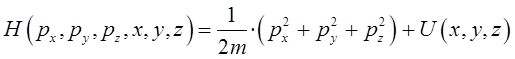
Зная вид гамильтониана в декартовой системе координат, преобразуем его в сферическую систему координат. Для этого запишем кинетическую энергию как функцию координат 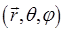и соответствующих скоростей 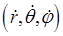путём подстановки производных 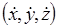в выражение для кинетической энергии:

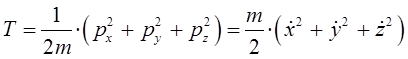
здесь:

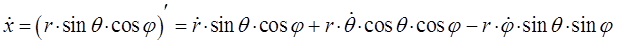
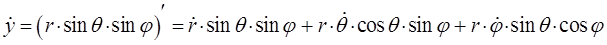
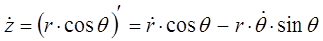
или после взятия производной функции, с последующим возведением в квадрат результатов дифференцирования, приходим к соответствующим промежуточным результатам для каждой из пространственных координат:

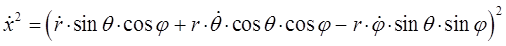
откуда:

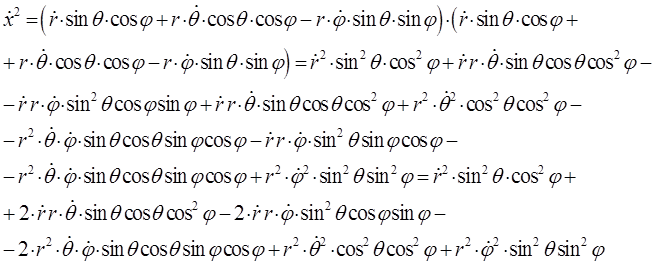
и аналогично:

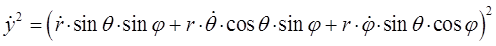
откуда: