Физические основы и предпосылки возникновения квантовой механики

Основы квантовой механики.

Не сразу удалось понять и сформулировать законы квантовой механики. Нужна была огромная смелость, чтобы сразу отказаться от старых, хорошо проверенных традиций классической физики. Классическая механика и электродинамика при попытке применения их к объяснению атомных явлений приводят к результатам, находящимся в резком противоречии с опытом. Наиболее ясно это стало видно при применении обычной электродинамики к модели атома, в котором электроны движутся вокруг ядра по классическим орбитам. При таком движении, как и при всяком ускоренном движении зарядов, электроны должны были бы непрерывно излучать электромагнитные волны. Излучая, электроны теряли бы свою энергию, что должно было бы привести, в конце концов, к их падению на ядро. Таким образом, согласно классической электродинамике, атом был бы неустойчивым, что ни в какой степени не соответствует действительности. Такое глубокое противоречие теории с экспериментом свидетельствует о том, что построение теории, применимой к атомным явлениям, - явлениям, происходящим с частицами очень малой массы в очень малых участках пространства, – требует фундаментального изменения в основных классических законах и представлениях. В качестве отправной точки для выяснения этих изменений удобно исходить из наблюдаемого на опыте явления – так называемой дифракции электронов. Оказалось, что при пропускании однородного пучка электронов через кристалл никеля (опыты Дэвиссона и Джермера), в прошедшем пучке обнаруживается картина чередующихся максимумов и минимумов интенсивности, вполне аналогичная дифракционной картине, наблюдаемой при дифракции электромагнитных волн. Таким образом, в некоторых условиях поведение материальных частиц, электронов, обнаруживает черты, свойственные волновым процессам, а потому механика, которой подчиняются атомные явления (так называемая квантовая или волновая механика) должна быть основана на представлениях о движении, принципиально отличных от представлений классической механики. В квантовой механике не существует понятия траектории частицы. Это обстоятельство составляет содержание так называемого принципа неопределённости – одного из основных принципов квантовой механики, открытого В. Гейзенбергом. Остановимся на особом характере взаимоотношения, в котором находятся квантовая и классическая механики. Обычно более общая теория может быть сформулирована логически замкнутым образом независимо от менее общей теории, являющейся её предельным случаем. Так, релятивистская механика может быть построена на основании своих принципов без всяких ссылок на ньютоновскую механику. Формулировка же основных положений квантовой механики принципиально невозможна без привлечения механики классической. Таким образом, квантовая механика занимает своеобразное положение в ряду физических теорий – она содержит классическую механику как свой предельный случай и в тоже время нуждается в этом предельном случае для самого своего обоснования. Так, в квантовой механике не существует понятия скорости частицы в классическом смысле этого слова, т.е. как предела, к которому стремится разность координат в два момента времени, делённая на интервал 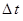между этими моментами. Однако в квантовой механике, тем не менее, может быть дано разумное определение скорости частицы в данный момент времени, которая при переходе к классической механике переходит в классическую скорость. В классической механике в каждый данный момент времени частица обладает определёнными координатами и скоростью. В квантовой же механике координаты и скорость электрона являются величинами, которые не могут быть измерены одновременно точно. Можно сказать, что координаты и скорость электрона – величины, не существующие одновременно. Полное описание состояния физической системы в классической механике осуществляется заданием в данный момент времени всех её координат и скоростей; по этим данным, уравнения движения полностью определяют поведение системы во все будущие моменты времени. В квантовой механике такое описание движения принципиально невозможно, поскольку координаты и соответствующие им скорости не существуют одновременно. Таким образом, описание состояния квантовой системы осуществляется меньшим числом величин, чем в классической механике, т.е. является менее подробным, чем классическое. Отсюда вытекает очень важное следствие относительно характера предсказаний, делаемых в квантовой механике. В то время как классическое описание достаточно для того, чтобы предсказать движение механической системы в будущем совершенно точным образом, менее подробное описание в квантовой механике, очевидно, не может быть достаточным для этого. Это значит, что если электрон находится в состоянии, описанном наиболее полным в квантовой механике образом, то, тем не менее, его поведение в следующие моменты времени принципиально неоднозначно. Поэтому квантовая механика не может делать строго определённых предсказаний относительно будущего поведения электрона. При заданном начальном состоянии электрона последующее измерение может дать различные результаты. Задача квантовой механики состоит лишь в определении вероятности получения того или иного результата при этом измерении. Разумеется, в некоторых случаях вероятность некоторого определённого результата измерения может оказаться равной единице, т.е. перейти в достоверность, так что результат данного измерения будет однозначным. Радикальное изменение физических представлений о движении в квантовой механике по сравнению с классической требует, естественно, и столь же радикального изменения математического аппарата теории. В этой связи, прежде всего, возникает вопрос о способе описания состояния квантовой системы. Так, если в классической механике состояние системы описывается заданием (в некоторый момент времени) всех её координат 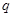и скоростей 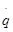, то в квантовой механике такое описание заведомо невозможно. Полное же описание состояния системы означает возможность предсказания вероятностей тех или иных результатов измерения координат (или других величин) системы. Как говорилось уже раньше, квантовая механика содержит в себе классическую в качестве предельного случая, тогда возникает вопрос о том, каким же образом осуществляется этот предельный переход? Такой переход происходит аналогично переходу от волновой к геометрической оптике. В волновой оптике электромагнитные волны описываются векторами электрического и магнитного полей, удовлетворяющими определённой системе линейных дифференциальных уравнений (уравнений Максвелла). В геометрической же оптике рассматривается распространение света по определённым траекториям – лучам. Вспомним, каким образом математически осуществляется этот переход. Итак, пусть u – какая-нибудь из компонент поля в электромагнитной волне. Её можно написать в виде:

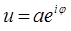
с вещественной амплитудой a и фазой j (последнюю называют в геометрической оптике эйконалом). Предельный случай геометрической оптики соответствует малым длинам волн, что математически выражается большой величиной изменения j на малых расстояниях; это означает, в частности, что фазу можно считать большой по своей абсолютной величине. Соответственно этому исходим из предположения, что предельному случаю классической механики соответствуют в квантовой механике волновые функции вида 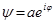, где а – медленно меняющаяся функция, а j принимает большие значения. Как известно, в механике траектория частиц может быть определена из вариационного принципа, согласно которому так называемое действие S механической системы должно быть минимальным (принцип наименьшего действия). В геометрической же оптике ход лучей определяется так называемым принципом Ферма, согласно которому должна быть минимальной «оптическая длина пути» луча, т.е. разность фаз в конце и начале пути. Исходя из этой аналогии, мы можем утверждать, что фаза волновой функции в классическом предельном случае должна быть пропорциональна механическому действию S рассматриваемой физической системы, т.е. должно быть S = const ^. j. Коэффициент пропорциональности называется постоянной Планка и обозначается буквой 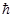и имеет размерность действия, поскольку j безразмерна. Таким образом, волновая функция квазиклассической физической системы имеет следующий вид:

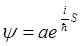
Постоянная Планка играет фундаментальную роль во всех квантовых явлениях. Её относительная величина (по сравнению с другими величинами той же размерности) определяет «степень квантованности» той или иной физической системы или величины. Переход от квантовой к классической механике, соответствуя большой фазе, может быть формально описан как переход к пределу 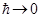(подобно тому, как переход от волновой к геометрической оптике соответствует переходу к пределу равной нулю длины волны, 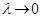). В общем случае движение, описываемое волновой функцией, отнюдь не переходит в движение по определённой траектории. Её связь с классическим движением заключается в том, что если в некоторый начальный момент волновая функция, а с нею и распределение вероятностей координат заданы, то в дальнейшем это распределение будет «перемещаться» так, как это полагается по законам классической механики. Для того чтобы получить движение по определённой траектории, надо исходить из волновой функции особого вида, заметно отличной от нуля лишь в очень малом участке пространства (так называемый волновой пакет). При этом размеры этого участка асимптотически стремятся к нулю вместе с 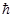, тогда можно утверждать, что в квазиклассическом случае волновой пакет будет перемещаться в пространстве по классической траектории частицы. Вся квантовая механика строится на совокупности постулатов, справедливость которых находит своё выражение в согласии с данными, полученными экспериментальным путём, а уравнение Шрёдингера играет в ней такую же роль, что и уравнение Ньютона в классической механике, и уравнения Максвелла в классической электродинамике. Описание состояния частицы в квантовой механике характеризуется волновой функцией, являющейся решением волнового уравнения. Эта функция описывает стационарные состояния, указывая распределение вероятности нахождения частицы в пространстве, не зависящее от времени. Каждому стационарному состоянию физической системы отвечает определённое значение энергии, вследствие чего для частицы или системы частиц существует набор физически допустимых значений энергии. Существование стационарных состояний и дискретность значений энергии являются следствием волновых свойств частиц, а не постулатом, как в это имело место в теории Бора.