Задание 1. Найдите общее решение дифференциального уравнения первого порядка с разделяющимися переменными:
1.1 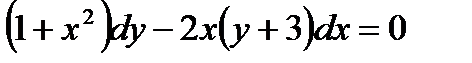
1.2 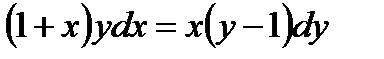
1.3 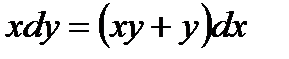
1.4 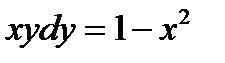
1.5 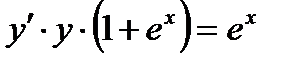
Задание 2. Найдите общее решение однородного дифференциального уравнения первого порядка:
2.1 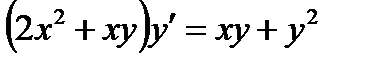
2.2 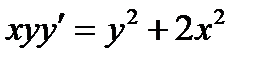
2.3 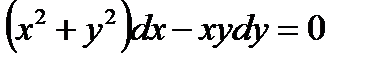
2.4 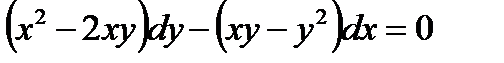
2.5 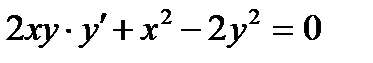
Задание 3. Найдите общее и частное решения линейного дифференциального уравнения первого порядка:
3.1 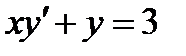 , если
, если 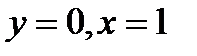
3.2 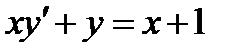 , если
, если 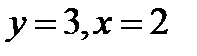
3.3 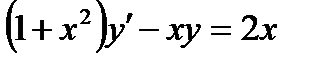 , если
, если 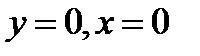
3.4 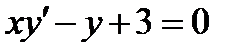 , если
, если 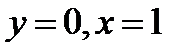
3.5 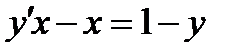 , если
, если 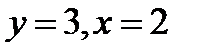
Задание 4. Найдите общее решение линейного однородного дифференциального уравнение второго порядка с постоянными коэффициентами:
4.1 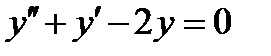
4.2 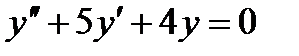
4.3 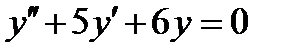
4.4 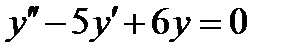
4.5 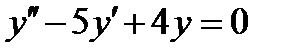
Задание 5. Найдите общее и частное решения линейного однородного дифференциального уравнение второго порядка с постоянными коэффициентами:
5.1 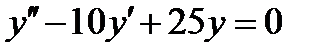 , если
, если 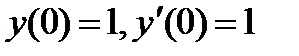
5.2 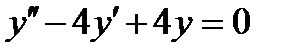 , если
, если 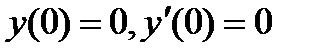
5.3 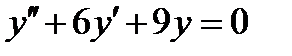 , если
, если 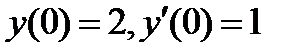
5.4 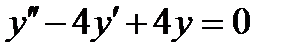 , если
, если 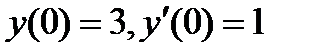
5.5 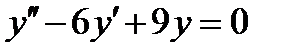 , если
, если 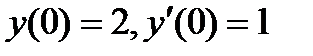
Задание 6. Найдите общее и частное решения линейного однородного дифференциального уравнение второго порядка с постоянными коэффициентами:
6.1 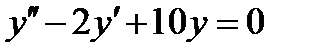 , если
, если 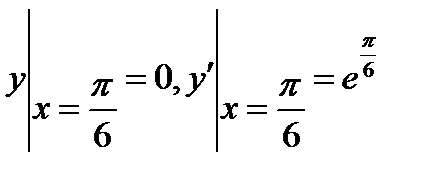
6.2 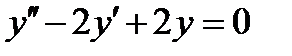 , если
, если 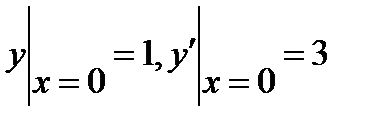
6.3 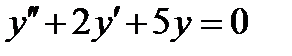 , если
, если 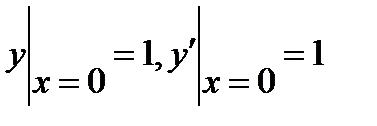
6.4 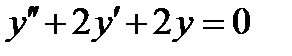 , если
, если 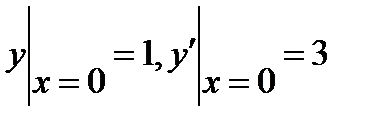
6.5 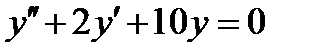 , если
, если 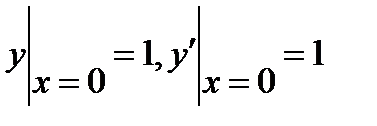
Вопросы для самоконтроля
- Какое уравнение называется дифференциальным?
- Перечислите известные вам типы дифференциальных уравнений первого порядка. Приведите примеры.
- Чем частное решение отличается от общего?
- Может ли решение дифференциального уравнения: а) быть конечным; б) быть представлено в виде
 ?
? - Может ли ДУ первого порядка содержать: а) вторую производную искомой функции; б) искомую функцию; в) производную искомой функции; г) независимую переменную?
- Как записать в общем случае дифференциальное уравнение второго порядка?
- Что называется решением дифференциального уравнения второго порядка?
- Запишите в общем виде линейное дифференциальное уравнение второго порядка с постоянными коэффициентами.
- Что называется характеристическим уравнением?
- Напишите общее решение уравнения, когда его характеристическое уравнение не имеет действительных корней?
- Могут ли интегральные кривые ДУ: а) пересекаться; б) касаться?
- Может ли решение ДУ второго порядка: а) быть конечным; б) быть представлено в виде
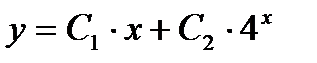 ?
?
 2015-03-22
2015-03-22 628
628








