1). Дифференциальные уравнения с разделяющимися переменными.
Дифференциальное уравнение с разделяющимися переменными имеет вид 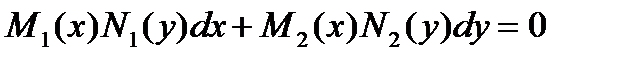 .
.
Пример1. Решить уравнение 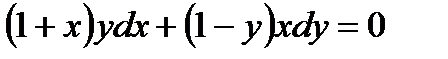 .
.
Решение. Разделим переменные, для чего члены уравнения поделим на ху: 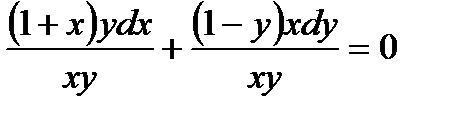 ,
, 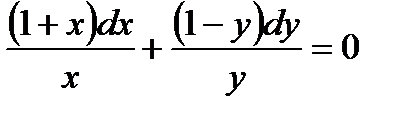
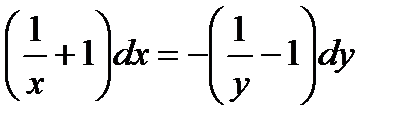 . Интегрируя почленно обе части уравнения, имеем
. Интегрируя почленно обе части уравнения, имеем 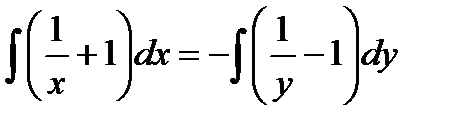 , откуда
, откуда 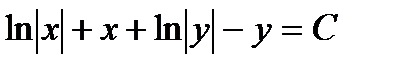 ,,
,, 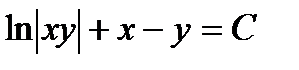 ,
, 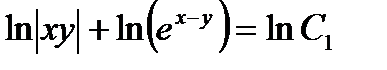 ,
, 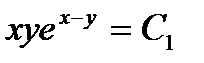 . Это общее решение данного дифференциального уравнения.
. Это общее решение данного дифференциального уравнения.
2). Однородные дифференциальные уравнения.
Дифференциальное уравнение первого порядка 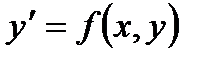 называется однородным, если его можно представить в виде
называется однородным, если его можно представить в виде 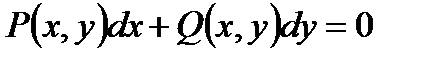 , где
, где 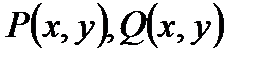 - однородные функции одинакового измерения.
- однородные функции одинакового измерения.
Пример 2. Найти частное решение уравнения 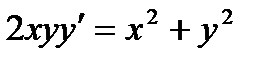 , если
, если 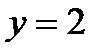 при
при 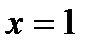 .
.
Решение. Записав данное уравнение в виде 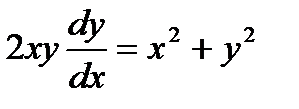 ;
; 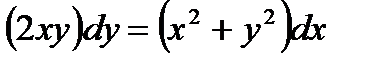 легко можно убедиться в том, что оно однородно. Положим у = zx, откуда dy = z dx + х dz. Подставляем значения у и dy в последнее уравнение:
легко можно убедиться в том, что оно однородно. Положим у = zx, откуда dy = z dx + х dz. Подставляем значения у и dy в последнее уравнение: 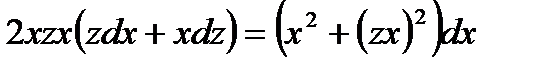 ;
; 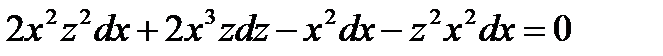 ;
; 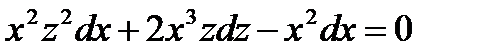 ;
; 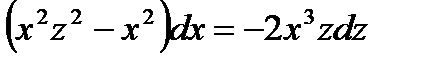 ;
; 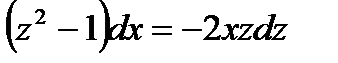 ;
; 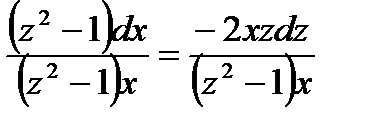 ;
; 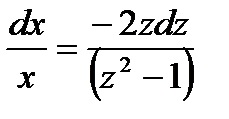 Интегрируя, получаем
Интегрируя, получаем 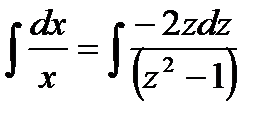 откуда
откуда 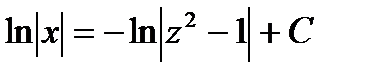 ;
; 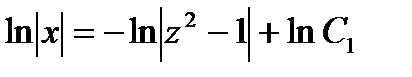 ;
; 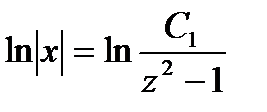 ;
; 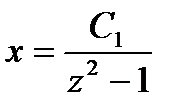 ;
; 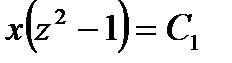 ;
; 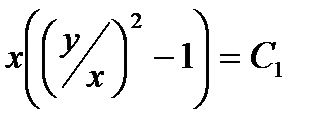
Подставив в найденное общее решение начальные условия, найдем 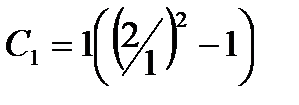 ;
; 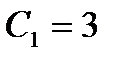
Итак, искомое частное решение будет 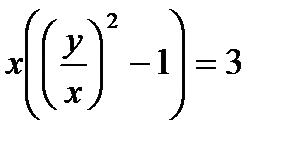 ;
; 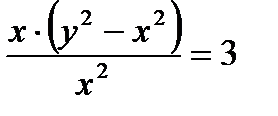 ; или
; или 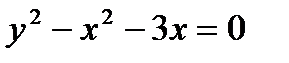
3) Линейные дифференциальные уравнения.
Линейными дифференциальными уравнениями называютсятакие уравнения, которые содержат неизвестную функцию и ее производную только в первой степени:
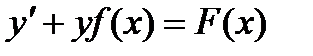 или
или 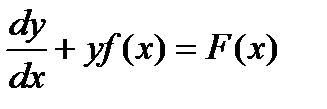 . Если
. Если 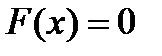 , то уравнение
, то уравнение 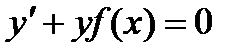 называется линейным уравнением без правой части.Для решения линейных уравнений пользуются подстановкой
называется линейным уравнением без правой части.Для решения линейных уравнений пользуются подстановкой 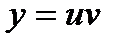 , где и и v — некоторые функции от х. Иначе говоря, разлагают у на два сомножителя. Следует иметь в виду, что эта операция не вполне определенная. Например, если
, где и и v — некоторые функции от х. Иначе говоря, разлагают у на два сомножителя. Следует иметь в виду, что эта операция не вполне определенная. Например, если 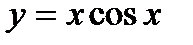 , то эту функцию можно разложить на множители бесчисленным множеством иных способов:
, то эту функцию можно разложить на множители бесчисленным множеством иных способов: 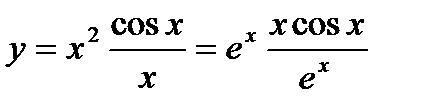 и т.д. Поэтому, полагая
и т.д. Поэтому, полагая 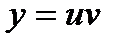 один из сомножителей можно выбрать произвольно.
один из сомножителей можно выбрать произвольно.
Пример 3. Решить уравнение 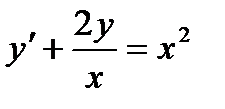
Решение. Здесь 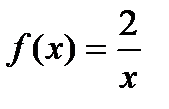 ,
, 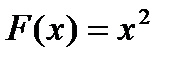 — уравнение линейное.
— уравнение линейное.
1)Полагаем 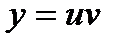 , тогда
, тогда 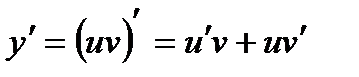 . Заменяя
. Заменяя 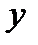 и
и 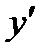 их значениями, получим:
их значениями, получим: 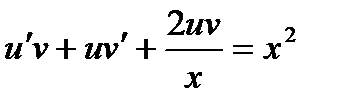 . Вынося во втором и третьем слагаемом и за скобки, найденное уравнение перепишем так:
. Вынося во втором и третьем слагаемом и за скобки, найденное уравнение перепишем так: 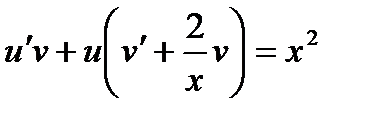 (1)
(1)
2)Выберем v так, чтобы выражение в скобках обратилось в нуль. Это справедливо, так как сомножитель в равенстве 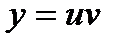 берем произвольно. Тогда получим:
берем произвольно. Тогда получим: 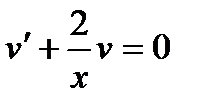 или
или 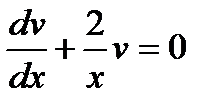
Разделим переменные: 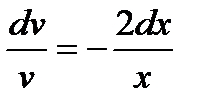 ,
, 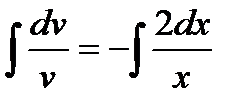 Или
Или 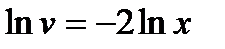 .Произвольную постоянную С можно не писать (в данном случаеберем постоянную, равную 0):
.Произвольную постоянную С можно не писать (в данном случаеберем постоянную, равную 0): 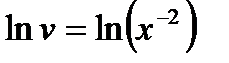 ,
, 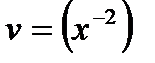 ,
, 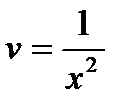
3)Теперь уравнение (1) примет вид 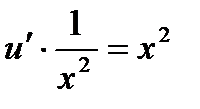 ,
, 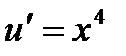 ,
,
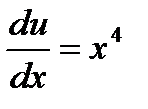 ,
, 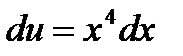 ,
, 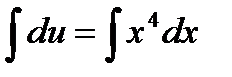 ,
, 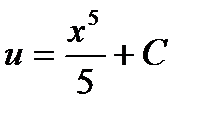 . Здесь С писать обязательно, иначе получится решение не общее а частное.
. Здесь С писать обязательно, иначе получится решение не общее а частное.
4).Теперь найдем искомую функцию, помня, что 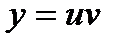 , а
, а 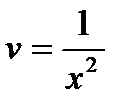 и
и 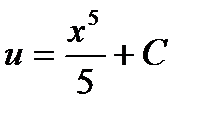 :
: 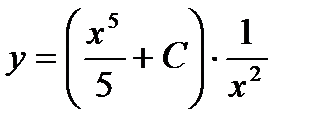 ,
, 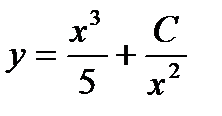
Дифференциальные уравнения II порядка.
Определение. Уравнение, связывающее независимую переменную, неизвестную функцию, ее первую производную, а тек же вторую производную от искомой функции, называется дифференциальным уравнением второго порядка.
В общем случае дифференциальное уравнение второго порядка можно записать в виде F (х, у, у',y") = 0, где у= у(х) -искомая функция.
Одним из представителей дифференциальных уравнений второго порядка является линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Уравнение вида 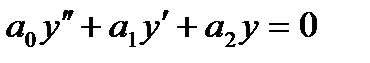 (1), где
(1), где 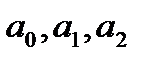 - действительные числа
- действительные числа  , называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Чтобы решить уравнение (1), нужно решить характеристическое уравнение
, называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Чтобы решить уравнение (1), нужно решить характеристическое уравнение 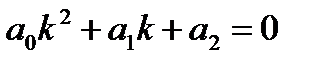 (2)
(2)
При решении характеристического уравнения (2) возможны три случая, в зависимости от которых строится общее решение данного дифференциального уравнения (1):
| Корни уравнения(2) | Частные решения уравнения (1) | Общее решение уравнения (1) |
Действительные и различные: 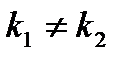 | 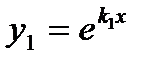 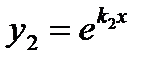 | 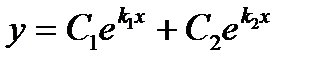 |
Равные: 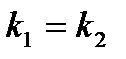 | 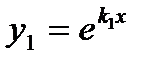 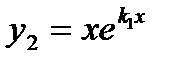 | 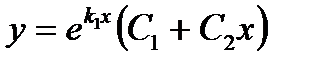 |
Комплексно-сопряженные: 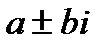 | 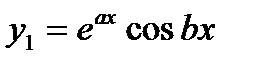 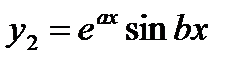 | 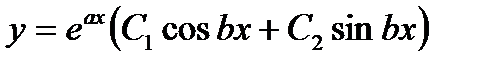 |
Пример 1. Найти общее решение дифференциального уравнения 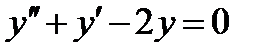
Решение. Характеристическое уравнение имеет вид 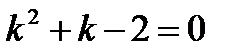 . Его корни
. Его корни 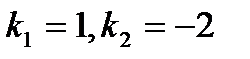 . Так как корни действительные и различные, то общее решение записывается в виде
. Так как корни действительные и различные, то общее решение записывается в виде 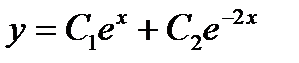 .
.
Пример 2. Найти общее решение дифференциального уравнения 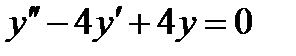
Решение. Характеристическое уравнение 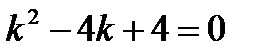 имеет равные корни
имеет равные корни 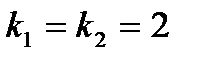 . Следовательно, общее решение данного уравнения таково:
. Следовательно, общее решение данного уравнения таково:  .
.
Пример 3. Найти общее решение дифференциального уравнения 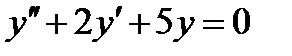
Решение. Характеристическое уравнение 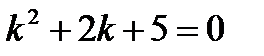 имеет комплексно-сопряженные корни:
имеет комплексно-сопряженные корни: 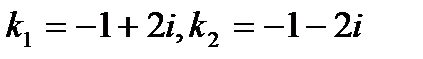 . Таким образом, общее решение уравнения записывается в виде
. Таким образом, общее решение уравнения записывается в виде 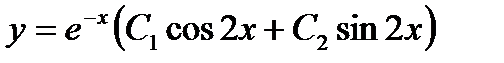
Пример 4. Найти частное решение уравнения 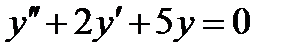 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 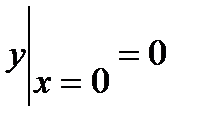 ,
, 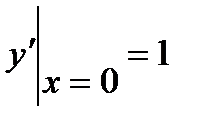
Решение. Общее решение уравнения записывается в виде
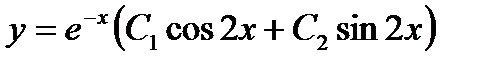
Найдем частное решение, которое удовлетворяет заданным начальным условиям. Из первого условия следует, что 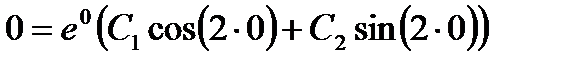 ,
, 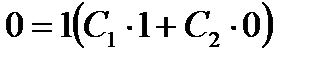 , откуда
, откуда 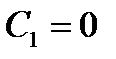 . Учитывая, что
. Учитывая, что 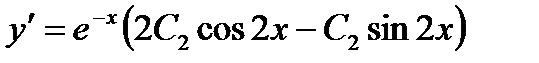 , и используя второе начальное условие, находим
, и используя второе начальное условие, находим 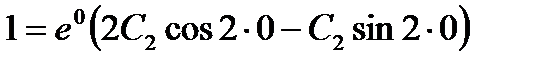 ,
, 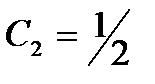 . Следовательно, искомое частное решение имеет вид
. Следовательно, искомое частное решение имеет вид 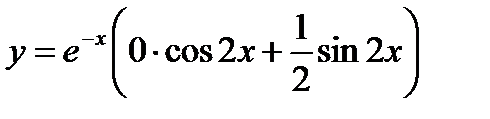 ,
, 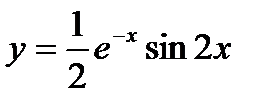
Пример 5. Найти интегральную кривую дифференциального уравнения 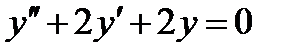 , проходящую через точку
, проходящую через точку 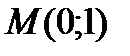 и касающуюся в этой точке прямой
и касающуюся в этой точке прямой 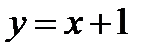 .
.
Решение. Характеристическое уравнение имеет вид 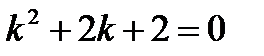 ; его корни
; его корни 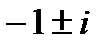 являются комплексно-сопряженными. Уравнение множества интегральных кривых запишется так
являются комплексно-сопряженными. Уравнение множества интегральных кривых запишется так 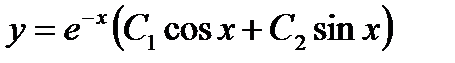 :
:
Найдем уравнение искомой интегральной кривой, для чего в равенства
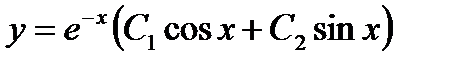 и
и 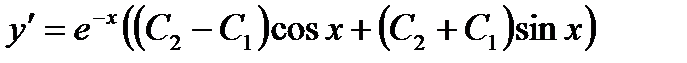 подставим значения у = 1 и углового коэффициента касательной
подставим значения у = 1 и углового коэффициента касательной 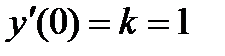 . В результате получим
. В результате получим 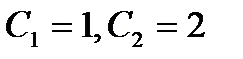 . Подставив эти значения в общее решение, получим
. Подставив эти значения в общее решение, получим 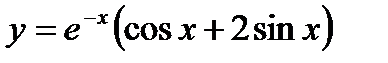 .
.
 2015-03-22
2015-03-22 3079
3079
