Формула прямоугольников. Пусть на отрезке [a;b], a<b задана непрерывная функция f(x)

Пусть на отрезке [a;b], a<b задана непрерывная функция f(x). Tpебуется вычислить интеграл 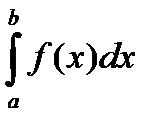, численно равный площади соответствующей криволинейной трапеции.

Разобьем основание этой трапе­ции, т. е. отрезок [a;b], на n равных частей (отрезков) длины 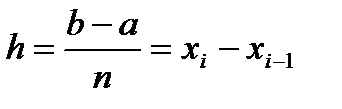(шаг разбиения) с помощью точек 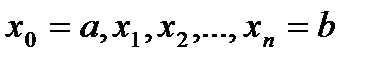. 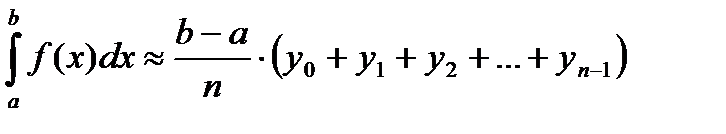-(1)- формула прямоугольников, где n – число равных отрезков, на которые разбит отрезок [a;b]

Формула трапеций

Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обыч­ной.

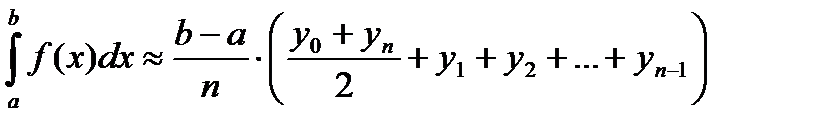-(2)- формула трапеций, где n – число равных отрезков, на которые разбит отрезок [a;b]