Уравнение Гамильтона-Якоби

Покажем теперь, что временное уравнение Шрёдингера, которое является основным динамическим законом квантовой механики, в пределе при 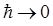автоматически переходит в основное уравнение классической механики. Отметим, однако, сначала, что та форма уравнения классической механики, в которую переходит уравнение Шрёдингера, в элементарных изложениях не встречается и поэтому нуждается в особом пояснении. Так, из классической механики известно, что уравнения движения частицы или системы частиц могут быть представлены в математически различных формах. Это или ньютоновы уравнения, или уравнения Лагранжа, особенно удобные для решения сложных задач в обобщённых координатах, или, наконец, гамильтоновы канонические уравнения. Все эти различные уравнения представляют собой с математической точки зрения системы дифференциальных уравнений: в случае ньютоновых или лагранжевых уравнений – второго порядка, – и первого порядка, но вдвое большего числа, – в случае гамильтоновых канонических уравнений. Решение этих уравнений приводит к выражениям координат и импульсов частиц в зависимости от времени. С интересующей нас точки зрения важно подчеркнуть, что все перечисленные формы уравнений движения являются обыкновенными дифференциальными уравнениями. В аналитической механике доказывается, однако, что решение системы гамильтоновых канонических уравнений может быть сведено к решению одного дифференциального уравнения в частных производных. Это уравнение в частных производных первого порядка по времени называется уравнением Гамильтона-Якоби. С его помощью могут решаться любые задачи классической механики. Конечно, решение простейших механических задач при помощи уравнения в частных производных выглядит несколько громоздко, однако при помощи этого уравнения могут быть решены сложные задачи небесной механики, к проблемам которой оно оказалось наилучшим образом приспособлено. Основное динамическое уравнение квантовой механики – общее уравнение Шрёдингера – по своей структуре, характеру и способу установления ближе всего подходит именно к уравнению Гамильтона-Якоби классической механики. Формально уравнение Гамильтона-Якоби может быть получено, если исходить из следующих соображений, придерживаясь следующего алгоритма. Напишем общее выражение закона сохранения энергии исходя из функции Гамильтона:

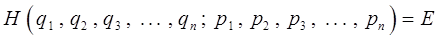
и далее произведём следующую замену:

где S есть некоторая функция обобщённых координат и времени – так называемая функция (или величина) действия. Она имеет размерность произведения энергии на время. Напомним, что ранее, при обсуждении вариационных принципов механики, нами были уже получены данные соотношения. Получаемое таким образом дифференциальное уравнение в частных производных для функции S и есть уравнение Гамильтона-Якоби:

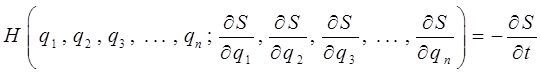
Общий интеграл уравнения в частных производных Гамильтона-Якоби должен быть выражен в виде произвольной функции независимых переменных. Однако обычно довольствуются отысканием, так называемого полного интеграла, представляющего собой выражение функции S в зависимости от времени, координат и такого числа независимых произвольных постоянных 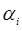, каково число обобщённых координат:

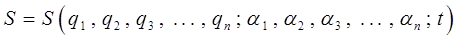
Если найден полный интеграл S, то координаты и функции времени найдутся из системы уравнений:

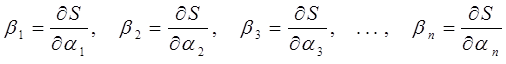
где 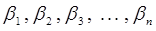– вторая группа произвольных постоянных. Импульсы получаются путём дифференцирования функции S по координатам в соответствии с условием:

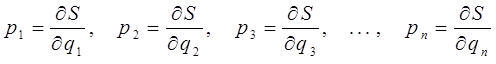
Две группы произвольных постоянных 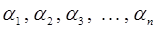и 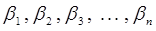, позволяют довести решение уравнения до конца. Рассмотрим случай одномерного движения в поле с потенциалом U. В этом случае выражение закона сохранения энергии будет иметь место, и гамильтониан равен полной энергии системы:

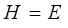
В декартовых координатах приведенное выше уравнение имеет вид:

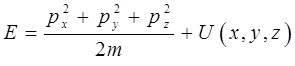
Произведя замену импульсов и времени по приведенной выше схеме, получаем уравнение Гамильтона-Якоби в явном виде:

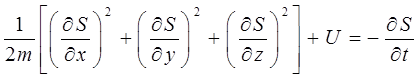
или в компактной форме, вводя представления о градиенте скалярной функции:

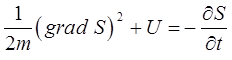
Последнее уравнение допускает интересную геометрическую интерпретацию, служащую основанием для аналогии между геометрической оптикой и механикой. Этой аналогией в своё время воспользовался Э. Шрёдингер, при построении квантовой механики. Для того чтобы показать использование и границы применимости уравнения Гамильтона-Якоби при решении одномерной задачи, воспользуемся задачей о линейном гармоническом осцилляторе. Гамильтониан, записанный в обобщённых координатах и импульсах, определяется выражением:

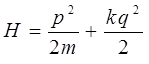
где 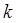– силовая постоянная квазиупругой силы. Поскольку гамильтониан в таком случае будет являться полной энергией системы, тогда:

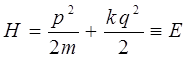
Соответствующее уравнение Гамильтона-Якоби будет поэтому:

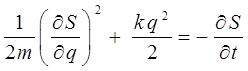
Так как время в этом уравнении в явном виде входит только в правой части, то решение (полный интеграл) можно искать в виде:

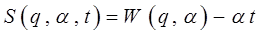
где W представляет собой так называемое укороченное действие. Подставляя это решение в уравнение:

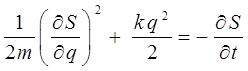
получаем уравнение для функции W:

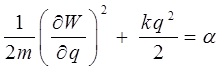
Отсюда находим:

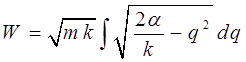
или после подстановки в уравнение:

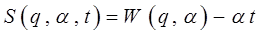
получаем:

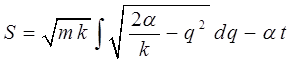
Вычислять входящий сюда интеграл нет необходимости, так как нас интересует в данном случае не величина действия S, а её частная производная по 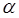. Так, имеем:

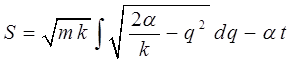
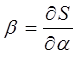
или после соответствующей подстановки с последующим дифференцированием:

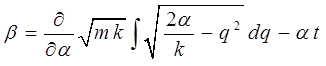
имеем в окончательном виде:

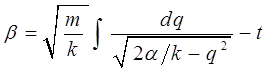
В правую часть полученного выражения входит хорошо известный табличный интеграл, и мы получаем после элементарных преобразований:

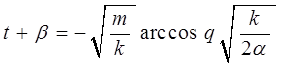
откуда, решая полученное уравнение, находим соответственно:

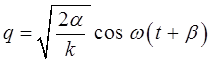
где

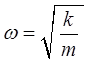
Таким образом, пользуясь уравнением Гамильтона-Якоби, мы пришли к формуле, описывающей гармоническое колебательное движение. Этого примера достаточно, чтобы показать, что задачи механики, в том числе, конечно, и простые, можно решать, пользуясь уравнением Гамильтона-Якоби – для функции S, зависящей от координат и времени. Действие S и функция W, называемая также часто укороченным действием, входят в вариационную формулировку основных законов механики на основании принципа наименьшего действия (принципа Гамильтона) и соответственно принципа укороченного действия. Принцип наименьшего действия в форме Эйлера-Лагранжа часто называют также принципом Мопертюи. Обратимся теперь к квантовой механике. Так, общее уравнение Шрёдингера можно формально получить по той же схеме, что и классическое уравнение Гамильтона-Якоби. Для этого запишем уравнение, выражающее закон сохранения энергии:

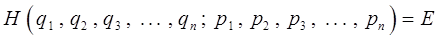
и заменяем в его левой части величины обобщённых координат 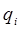и импульсов 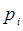операторами по обычной схеме:

причём:

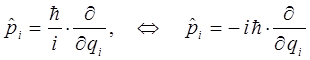
В правой же части величину полной энергии заменяем оператором дифференцирования по времени:

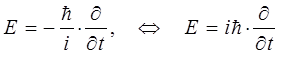
Сравним теперь схемы составления уравнения Гамильтона-Якоби в классической механике и уравнения Шрёдингера, содержащего время, в квантовой механике. Так, при составлении уравнения Гамильтона-Якоби в классической механике величины энергии 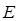, обобщённых координат 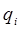и импульсов 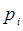заменяем величинами:

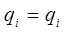
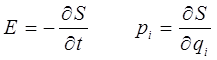
подставляя данные величины в уравнение:

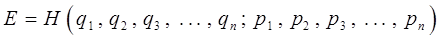
имеем соответственно:

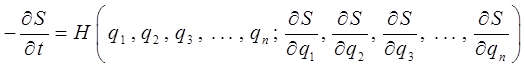
Аналогично, при составлении уравнения Шрёдингера в квантовой механике величины энергии 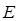, обобщённых координат 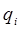и импульсов 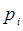заменяем:

причём:

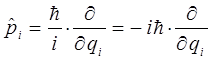
и соответственно:

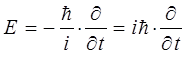
Подставляя данные величины в уравнение:

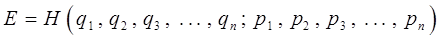
имеем соответственно:

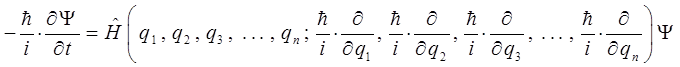или что то же самое:

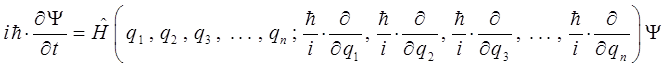
Полученные таким образом уравнение Гамильтона-Якоби и уравнение Шрёдингера можно переписать далее в виде:

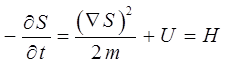
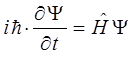
Используя предложенную выше схему, составим общее уравнение Шрёдингера для одной частицы. Используя декартовую систему координат, запишем аналитическое выражение закона сохранения энергии:

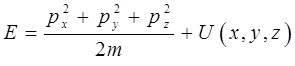
Производя в этом выражении замену по общей схеме, применяя операторы к функции координат и времени 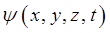, получаем искомое уравнение. Так, по определению имеем:

и соответственно:

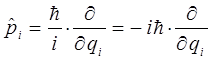
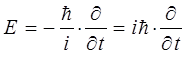
Делая замены в полученном выражении в соответствии с приведенной выше схемой, будем иметь соответственно:

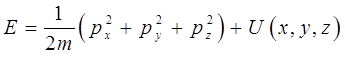
или после соответствующих подстановок:

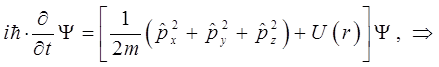
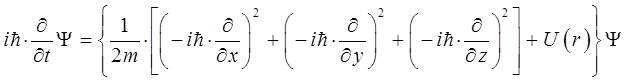
откуда следует:

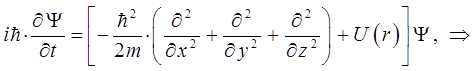
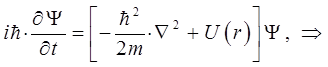
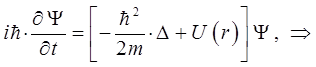
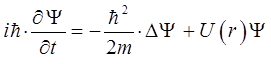
или в окончательном виде:

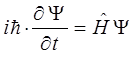
Таким образом, мы видим, что действительно имеется формальная аналогия между способами установления основного динамического уравнения классической механики – уравнения Гамильтона-Якоби, и основного динамического уравнения квантовой механики – уравнения Шрёдингера. Эта аналогия пока что является совершенно формальной в том смысле, что она ограничивается схемой написания обоих уравнений и е даёт абсолютно никаких указаний на их внутреннюю связь. Покажем, что такая связь, тем не менее, существует и что уравнение Шрёдингера переходит именно в уравнение Гамильтона-Якоби в пределе при , то есть при условии, когда, согласно принципу соответствия, законы квантовой механики должны переходить в законы классической физики. Для того чтобы это доказать, будем искать решение уравнения Шрёдингера:

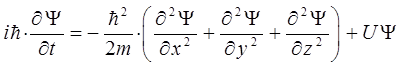
в виде:

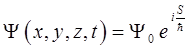
где

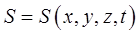
функция, имеющая размерность действия и 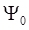– постоянная, характеризующая распределение стоячих волн в пространстве. Найдём производные:

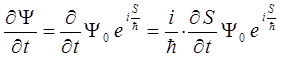
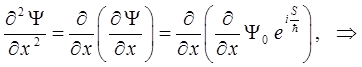
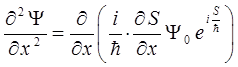
и таким образом:

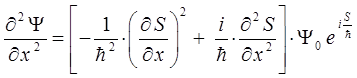
Аналогичные формулы имеют место для вторых производных по двум другим пространственным координатам y и z. Подставляя эти выражения для производных в уравнение Шрёдингера, получим после соответствующих преобразований и сокращения на общий множитель 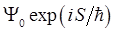уравнение Гамильтона-Якоби. Для того чтобы избежать громоздкости выкладок, будем рассматривать задачу по координатно, получив изначально промежуточные результаты, которые далее сложим и получим искомое уравнение для трёх пространственных координат. Итак, считаем исходным уравнение Шрёдингера вида:

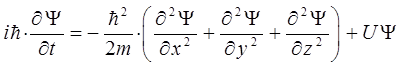
В целях большей наглядности и упрощения последующих выкладок, рассмотрим его по координатно, т.е. в виде системы трёх уравнений, каждое из которых отвечает одной из трёх возможных в данном случае координат, т.е.

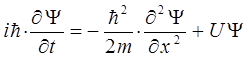
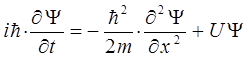
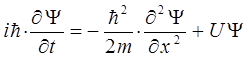
Ранее нами было установлено, что:

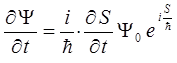
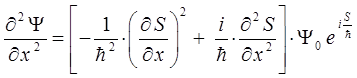
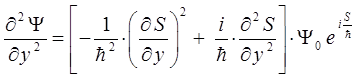
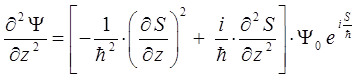
подставляя данные выражения в каждое из имеющихся у нас уравнений, будем иметь соответственно:

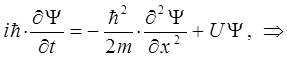
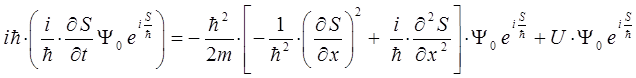
и таким образом:

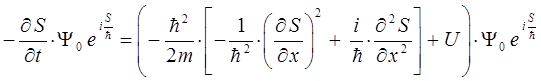
Сокращая правую и левую части полученного выражения на один и тот же множитель, будем иметь:

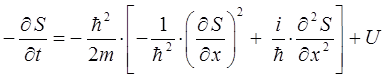
откуда соответственно:

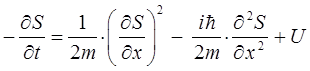
Аналогичные выражения очевидно можно будет получить и для двух других пространственных координат:

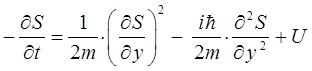
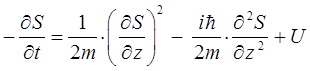
Складывая промежуточные результаты по каждой из координат между собой, будем иметь соответственно:

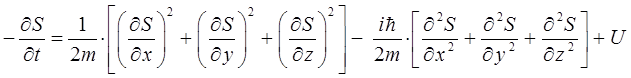
учитывая, что:

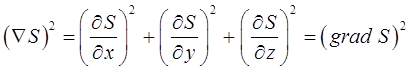
а также:

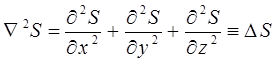
полученное нами выше уравнение:

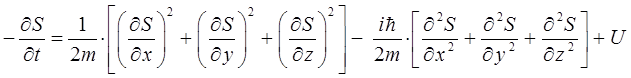
может быть переписано и представлено к виду:

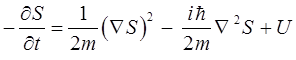
или в эквивалентной форме:

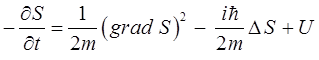
Полученное уравнение представляет собой квантовое уравнение Гамильтона-Якоби, которое отличается от классического тем, что содержит типично квантовую поправку – член вида:

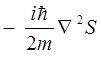
В ряде случаев полученное выше уравнение Гамильтона-Якоби может быть преобразовано далее к виду:

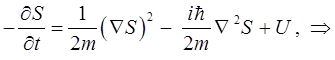
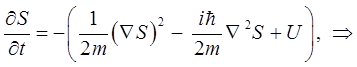
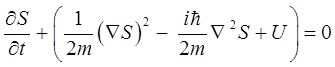
и в окончательном виде:

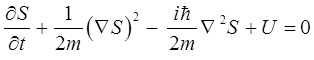
В качестве предельного случая, соответствующего классической механике принимается, что 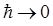. В этом случае квантовое уравнение:

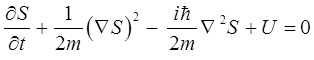
переходит в классическое:

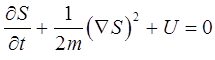
или для случая одного измерения:

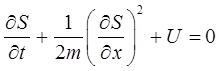
Полученное выше уравнение:

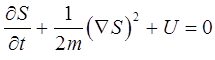
или его частный случай:

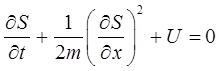
представляет уравнение Гамильтона-Якоби классической механики. Необходимо отметить, что с математической точки зрения условие 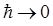является, по меньшей мере, безграмотным. Это связано с тем, что постоянная 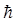– фундаментальная физическая константа и никуда стремиться не может. Более корректным будет являться требование малости квантового члена по сравнению с остальными составляющими квантового уравнения Гамильтона-Якоби.