Пример 3. Пусть заданы структурная схема и параметры системы

Пусть заданы структурная схема и параметры системы:

^{u 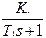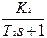y} K₁=2, K₂=0.5,

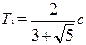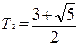+ - , с.

1. Определим передаточную функцию системы по структурной схеме:

.

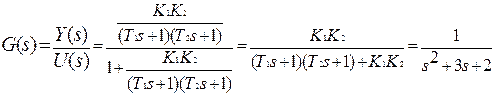2. Построим схему в переменных состояния методом прямого программирования

(схема моделирования канонической формы управляемости)

,

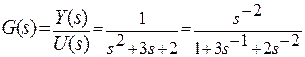отсюда 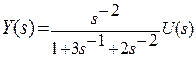, обозначим ,

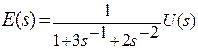тогда .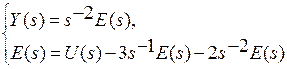

Схема переменных состояния имеет вид Эквивалентная схема

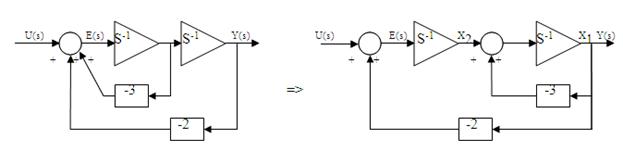
3. Построим граф системы по эквивалентной схеме в переменных состояния.

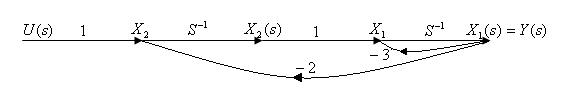
Сигнальный граф – диаграмма, состоящая из узлов, соединенных между собой отдельными направленными ветвями.

4. Определим передаточную функцию системы по формуле Мейсона:

,

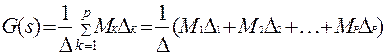где р - число прямых путей,

Δ=1 – (сумма коэффициентов передачи всех отдельных контуров) + (сумма произведений коэффициентов передачи всех возможных комбинаций не касающихся контуров, взятых по два) -

- (сумма произведений коэффициентов передачи всех возможных комбинаций не касающихся контуров, взятых по три) + (сумма произведений коэффициентов передачи всех возможных комбинаций не касающихся контуров, взятых по четыре) – (…),

М_К – коэффициент передачи k- го прямого пути,

Δ_К – значение Δ для той части графа, которая не касается k- го прямого пути.

,

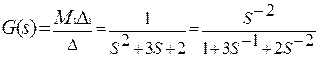Δ₁=1; М₁=1·S^-1·1·S^-1; Δ=1 - [ - 3S^-1 + (- 2S^-1·1·S^-1)].

5. Запишем уравнения состояния по графу системы.

Система дифференциальных уравнений:

· В обобщенном матричном виде: 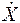=Ax + Bu,

Y=Cx + Du, (1)

где A – матрица коэффициентов;

В – матрица входа;

С – матрица выхода;

D – матрица обхода;

· В форме Коши: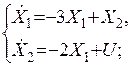

· В развернутом матричном виде: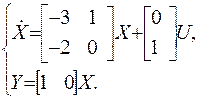

Решение (1) можно получить, применив преобразование Лапласа:

sX(s)-X(0)=AX(s)+BU(s); сгруппируем члены уравнения

sX(s)-AX(s)=X(0)+BU(s), тогда (sI-A)X(s)=X(0)+BU(s), решение получим в виде

X(s)=(sI-A)^-1X(0)+(sI-A)^-1BU(s);(2)

(sI-A)^-1=Ф(s).

Ф(t)=L^-1[Ф(s)]=e^At – матричная экспоненциальная функция описывает свободное движение

системы и называется фундаментальной матрицей или переходной матрицей состояния.

6. Определение матрицы перехода.

С этой целью сначала найдем матрицу

.

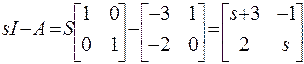Чтобы найти обратную матрицу, сформируем присоединенную матрицу

,

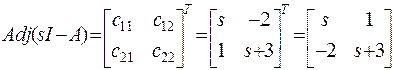где С_ij=(-1)^i+jm_ij – алгебраическое дополнение, а m_ij – миноры матрицы sI-A, и вычислим определитель

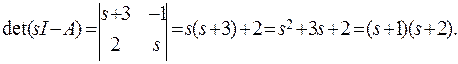
Тогда обратная матрица будет получена путем деления присоединенной матрицы на определитель det(sI-A):

.

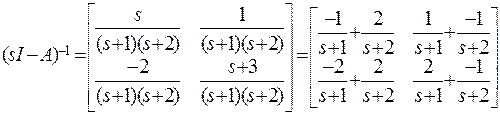Матрицу перехода получим с помощью обратного преобразования Лапласа:

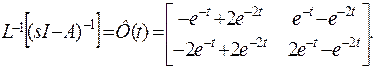
Для систем n–го порядка размерность матрицы перехода равна (n×n).

7. Отыскание полного решения уравнений состояния.

Предположим, что на вход системы подано единичное ступенчатое воздействие.

Тогда U(s) = 1/s, и второй член в выражении (2) принимает вид

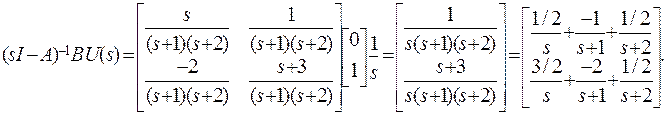
Применяя обратное преобразование Лапласа, получим:

.

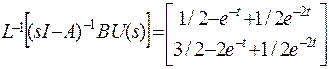Полное решение уравнения состояния имеет вид

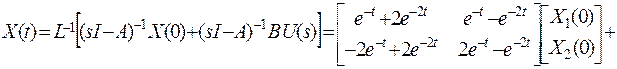
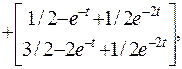
и переменные состояния равны:

X₁(t)=(-e^-t+2e^-2t)X₁(0)+(e^-t-e^-2t)X₂(0)+1/2-e^-t+1/2e^-2t=y(t)

и

X₂(t)=(-2e^-t+2e^-2t)X₁(0)+(2e^-t-e^-2t)X₂(0)+3/2-2e^-t+1/2e^-2t.

Для свободного движения системы решение можно записать в виде

.

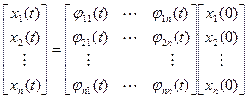Для того чтобы определить переходную матрицу состояния, необходимо начальные значения всех переменных состояния кроме одной положить равными нулю и вычислить реакцию каждой переменной состояния на это ненулевое значение. Иначе говоря, элемент 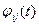представляет собой реакцию 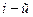переменной состояния на начальное значение 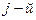переменной состояния при условии, что начальные значения всех остальных переменных состояния равны нулю.