Пример 2. Дано: процесс в объекте описывается уравнением

Дано: процесс в объекте описывается уравнением:

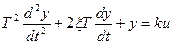. (3)

Требуется составить векторно-матричную форму записи дифференциального уравнения

и найти его решение (третья стандартная форма записи дифференциального уравнения

относительно переменных состояния).

Решение.

Применим метод фазовых переменных, т. е. введём в математическое описание объекта

n – переменных , .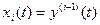

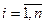Заметим, что в случае фазовых переменных матрица A имеет вид:

.

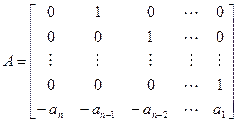Приняв 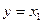, , 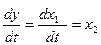(4)

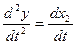, получим систему дифференциальных уравнений в форме

Коши, используя (3) и (4):

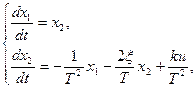
в матричной форме

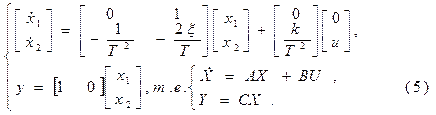
Решение (5) можно получить, применив преобразование Лапласа:

,

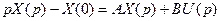сгруппируем члены уравнения

,

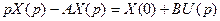отсюда

,

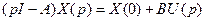решение получим в виде

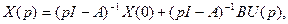
Φ(p) – фундаментальная матрица

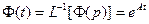– матричная экспоненциальная функция (переходная матрица состояния).

Схема моделирования:

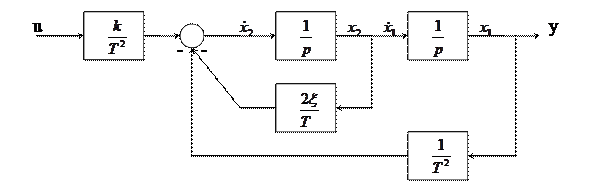
Сигнальный граф:

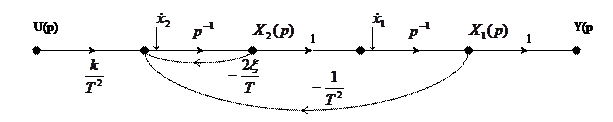
Сигнальный граф - диаграмма, состоящая из узлов, соединённых между собой отдельными направленными ветвями (дугами).