Способ построения модели в пространстве состояний по передаточной функции

Представление в пространстве состояний не единственно и определяется выбором вектора состояния. Оно определяется с точностью до постоянной матрицы, это значит, что умножая вектор состояния на различные невырожденные матрицы можно получить сколько угодно реализаций (моделей) в пространстве состояний.

Для одномерных систем (имеющих один вход и один выход) существует очень простой способ построения модели в пространстве состояний по передаточной функции. Пусть

.

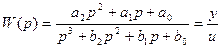Представим отношение 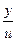в виде

, ,

.

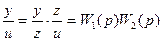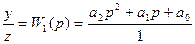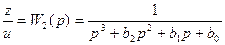Передаточная функция 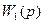соответствует дифференциальному уравнению

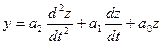, (1)

а 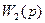- уравнению

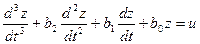. (2)

Вводя новые переменные состояния

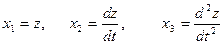
и учитывая связь между ними 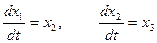, из (1) – (2) получаем систему

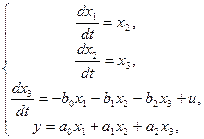
которая записывается в форме модели в пространстве состояний с матрицами

, , , , .

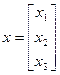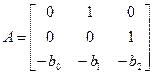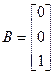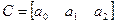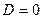Этот подход можно распространить и на случай передаточной функции любого порядка, однако при использовании окончательных формул следует помнить:

● старший коэффициент знаменателя должен быть равен 1, если это не так, числитель и знаменатель передаточной функции нужно разделить на это число;

● степень числителя должна быть ниже степени знаменателя, если они равны, нужно выделить целую часть (это будет матрица D) и строго правильную дробь;

● модель, соответствующая неправильной передаточной функции (у которой степень числителя выше степени знаменателя), не может быть представлена в стандартном пространстве состояний.