-> А- да, В- да
А- да, В- нет
А- нет, В- да
А- нет, В- нет
Ряд 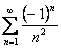
-> сходится абсолютно
сходится условно
расходится
ничего определенного сказать нельзя
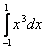 равен (набрать число)
равен (набрать число)
-> 0
Шестой член прогрессии 2, 7, 12, … равен (наберите число)
-> 27
Функции 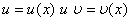 дифференцируемы в точке x. Установите соответствия между левыми и правыми частями правил дифференцирования
дифференцируемы в точке x. Установите соответствия между левыми и правыми частями правил дифференцирования
-> 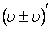 <->
<-> 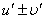
-> 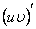 <->
<-> 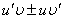
-> 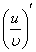 <->
<-> 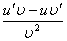
Интеграл 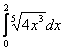 равен (набрать число с точностью до десятых)
равен (набрать число с точностью до десятых)
-> 2,5
Ряд Фурье функции f(x) = |х| (- 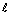 < x <
< x < 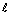 ), Т = 2ℓ, в точке х0 = ℓ сходится к значению
), Т = 2ℓ, в точке х0 = ℓ сходится к значению
-> ℓ
1
0
расходится в точке х0 = ℓ
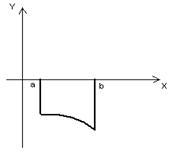
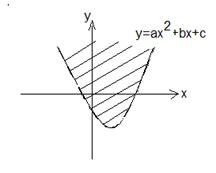
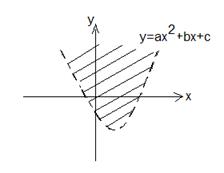
Одновременно трем условиям: y < 0; y¢ > 0; y² < 0 на отрезке [a, b] удовлетворяет график № (наберите № графика) 1) 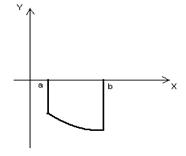 2)
2) 
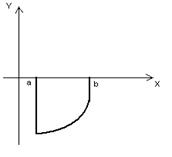
3) 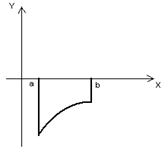 4)
4) 
-> 3
Производная функции 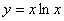 равна
равна
-> 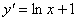
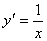
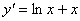
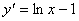
Прогрессия 2, 8, 14, … является
-> арифметической, a1= 2, d = 6
арифметической, a1= 6, d = 2
геометрической, b1= 2, q = 4
геометрической, b1= 4, q = 2
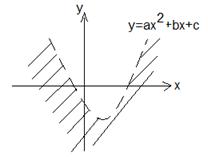
Множество А = 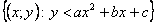 изображено на рисунке
изображено на рисунке
-> 
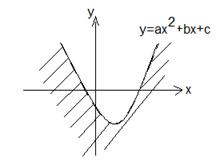
Производная функции 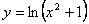 равна
равна
-> 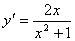
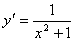
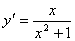
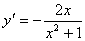
Функция z = (x + 4)4 + (y – 1)3 имеет
-> стационарную точку (–4, 1)
экстремум
в точке (–4, 1) минимум
в точке (–4, 1) максимум
Установите соответствие между названием уравнения и его видом
-> уравнение с разделяющимися переменными <-> 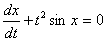
-> линейное дифференциальное уравнение первого порядка <-> 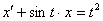
-> уравнение Бернулли <-> 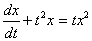
Средней кривизной кривой 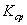 (плоской или пространственной) на участке между ее точками
(плоской или пространственной) на участке между ее точками 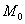 и
и 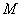 называется
называется
-> абсолютная величина отношения угла между касательными прямыми в точках 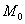 и
и 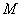 к длине дуги
к длине дуги 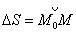
абсолютная величина угла между касательными прямыми в точках 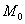 и
и 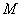
отношение угла между касательными в точках 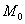 и
и 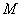 к
к 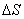
угол между касательными в 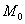 и
и 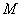
Частные производные функции z = x3 + xy равны
-> 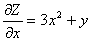
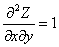
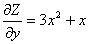
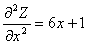
Установите соответствие между левыми и правыми частями таблицы
-> степенной ряд <-> 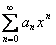
-> ряд Тейлора функции f(x) <-> 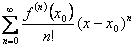
-> ряд Маклорена функции f(x) <-> 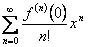
Установите соответствие между названием уравнения и его видом
-> уравнение с разделяющимися переменными <-> 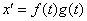
-> линейное дифференциальное уравнение первого порядка <-> 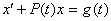
-> уравнение Бернулли <-> 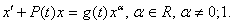
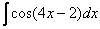 равен
равен
-> 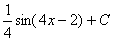
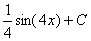
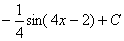
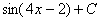
Точка с абсциссой 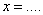 для функции
для функции 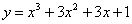 является точкой перегиба (наберите число)
является точкой перегиба (наберите число)
-> -1
Корни характеристического уравнения для 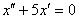 равны
равны 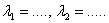 (набрать целые числа или ноль в порядке возрастания через запятую)
(набрать целые числа или ноль в порядке возрастания через запятую)
-> –5,0
Кривая расположена в некоторой плоскости. Тогда соприкасающаяся плоскость к ней в какой-то ее точке есть
-> та плоскость, в которой расположена кривая
касательная плоскость
та плоскость, которая соприкасается с кривой
та плоскость, которая касается кривой
Сумма первых десяти четных чисел 2, 4, 6, … равна (наберите число)
-> 110
 2015-03-22
2015-03-22 855
855








