Теоретическая часть. Интерполирование функций

Интерполирование функций

Цель работы: изучение и сравнительный анализ методов интерполяции функций; практическое решение задач интерполяции на ЭВМ.

Теоретическая часть

При разработке математического обеспечения ИТ часто прихо­дится иметь дело с функциями f (x), заданными в виде таблиц, ког­да известны некоторое конечное множество значений аргумента и соответствующие им значения функции. Аналитическое выражение функции f (x) при этом неизвестно, что не позволяет определять ее значения в промежуточных точках аргумента, отсутствующих в таблице. В таком случае решается задача интерполирования, которая формулируется следующим образом.

На отрезке [ a, b ] заданы n + 1 точки x ₀, x ₁,..., x_n, которые называются узлами интерполяции, и значения некоторой функ­ции f (x) в этих точках f (x ₀) = y ₀, f (x ₁) = y ₁,..., f (x_n) = y_n. Требуется построить интерполирующую функцию F (x), принимающую в узлах интерполяции те же значения, что и f (x), т.е. такую, что F (x ₀) = y ₀, F (x ₁) = y ₁,..., F (x_n) = y_n.

Геометрически это означает, что нужно найти кривую y = F (x) некоторого определенного типа, проходящую через заданную систему точек M_i (x_i, y_i) для i = 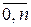. Полученная таким образом интерполяционная формула y = F (x) обычно используется для вычисления значений исходной функции f (x) для значений аргумента x, от­личных от узлов интерполяции. Такая операция называется интерполи­рованием функции f (x). При этом различают интерполирование в узком смысле, когда x принадлежит интервалу [ x ₀, x_n ], и экстраполирование, когда x не принадлежит этому интервалу.

В такой общей постановке задача интерполирования может иметь бесчисленное множество решений. Чтобы получить единственную функцию F (x), необходимо предположить, что эта функция не произвольная, а удовлетворяет некоторым дополнительным условиям.

В простейшем случае предполагается, что зависимость y = f (x) на каждом интервале (x_i, x_{i +1}) является линейной. Тогда для каж­дого участка (x_i, x_{i +1}) в качестве интерполяционной формулы y = F (x) используется уравнение прямой, проходящей через точки M_i (x_i, y_i) и M_{i +1}(x_{i +1}, y_{i +1}), которое имеет вид

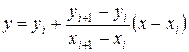. ( 1 )

При программировании процедур линейной интерполяции следует учитывать, что процесс решения задачи интерполирования с использованием формулы (1) включают два этапа: выбор интервала (x_i, x_{i +1}), которому принадлежит значение аргумента х; собственно вычисление значения y = F (x) по формуле (1).

На практике в качестве интерполирующей функции F (x) обычно используется алгебраический многочлен

P _n (x) = a ₀ + a ₁ x + a ₂ x ²+... + a_nxⁿ

степени не выше n, такой, что P_n (x ₀) = y ₀, P_n (x ₁) = y ₁,..., P_n (x_n) = y_n. Наиболее известными методами построения интерполяци­онного многочлена P_n (x) являются метод Лагранжа, итерационные и разностные методы.