Первая и вторая формулы Ньютона предполагают, что узлы интерполирования являются равноотстоящими. Однако, в общем случае функция f (x) может быть задана таблицей, в которой узлы находятся на произвольном расстоянии друг от друга 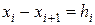 , где значения hi (i =
, где значения hi (i = 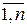 ) являются различными.
) являются различными.
При таких условиях первая и вторая интерполяционные формулы Ньютона неприменимы. В данном случае, для решения задачи интерполяции применяются не конечные, а разделенные разности.
Разделенная разность первого порядка определяется:
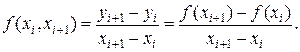
Для вычисления разделенных разностей высших порядков используется формула:
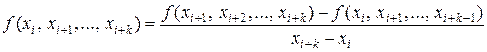
Разделенные разности удобно представлять диагональной таблицей, вид которой для n = 4 соответствует табл. 2.
Таблица 2
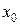 | 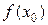 | 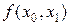 | 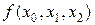 | 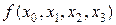 | 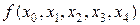 | |
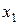 | 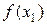 | |||||
 | ||||||
 | 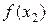 | 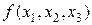 | ||||
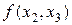 | 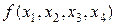 | |||||
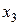 | 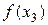 | 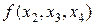 | ||||
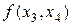 | ||||||
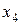 | 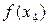 | |||||
Интерполяционный многочлен Ньютона, использующий разделенные разности, имеет вид:
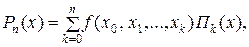
где 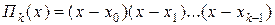 , Пk (x) = 1.
, Пk (x) = 1.
Представленная формула позволяет повышать точность вычислений постепенно, добавляя разделенные разности более высоких порядков. Следует отметить, что при этом все полученные результаты сохраняются, т.е. не вычисляются заново, а только наращиваются. Это следует из соотношения
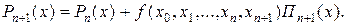
Оценка погрешности интерполирования выполняется по формуле
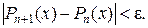
 2015-03-22
2015-03-22 876
876








