Глава 3
УРАВНЕНИЯ ДВИЖЕНИЯ ГАЗА
КАК СПЛОШНОЙ СРЕДЫ
Уравнения движения выводятся исходя из закона сохранения массы, закона изменения количества движения, закона сохранения энергии, уравнения термодинамического состояния и уравнения напряженного состояния.
Применим эти законы к массе жидкости m, находящейся в момент времени t в некотором произвольно выделенном объеме V. Будем считать, что внутри объема нет ни источников, ни стоков.
Уравнение неразрывности
Согласно закону сохранения массы для изолированной системы, масса жидкости m, которая находилась в момент времени t в рассматриваемом объеме, будет оставаться неизменной при ее движении. То есть 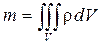 и
и 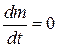 .
.
 Изменение массы при движении может происходить как за счет изменения плотности
Изменение массы при движении может происходить как за счет изменения плотности 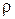 с течением времени, так и за счет изменения объема V, который может занимать рассматриваемая масса жидкости в следующий момент времени. Изменение массы за счет изменения плотности запишется как
с течением времени, так и за счет изменения объема V, который может занимать рассматриваемая масса жидкости в следующий момент времени. Изменение массы за счет изменения плотности запишется как 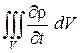 .
.
Найдем изменение массы за счет изменения объема. Элемент поверхности dS рассматриваемого объема переместится за время 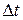 на расстояние
на расстояние 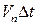 (рис. 3.1); за счет перемещения элемента поверхности объем изменится в единицу времени на
(рис. 3.1); за счет перемещения элемента поверхности объем изменится в единицу времени на 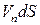 . Тогда изменение массы равно
. Тогда изменение массы равно 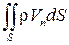 . Поскольку суммарное изменение массы равно нулю, то получаем
. Поскольку суммарное изменение массы равно нулю, то получаем 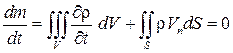 – закон сохранения массы в интегральной форме.
– закон сохранения массы в интегральной форме.
Преобразуем интеграл по площади в интеграл по объему с помощью формулы Остроградского–Гаусса:
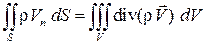 .
.
Объединяя интегралы, получим 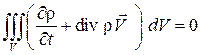 . В силу произвольности элементарного объема
. В силу произвольности элементарного объема 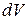 это равенство возможно, если подынтегральное выражение равно нулю, т. е. если
это равенство возможно, если подынтегральное выражение равно нулю, т. е. если
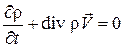 . (3.1)
. (3.1)
Выражение (3.1) представляет собой закон сохранения массы в дифференциальной форме, или иначе – уравнение неразрывности для неустановившегося движения сжимаемой жидкости. Для установившегося движения сжимаемой жидкости уравнение неразрывности имеет вид
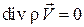 . (3.1а)
. (3.1а)
Приведем уравнение (3.1) к другой форме, произведя следующие преобразования:
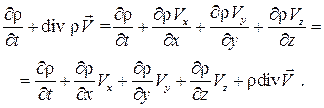
Так как 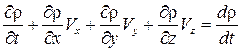 , то уравнение неразрывности примет вид
, то уравнение неразрывности примет вид
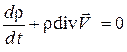 . (3.1б)
. (3.1б)
В случае движения несжимаемой жидкости (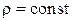 ) запись уравнения неразрывности еще более упростится:
) запись уравнения неразрывности еще более упростится:
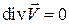 . (3.1в)
. (3.1в)
Если движение несжимаемой жидкости потенциальное, то проекции вектора скорости на координатные направления можно записать через потенциал вектора скорости 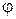 как
как
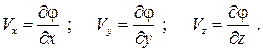
Тогда 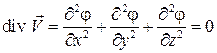 . Так как
. Так как 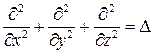 – это оператор Лапласа, то уравнение неразрывности для случая потенциального движения несжимаемой жидкости преобразуется в уравнение Лапласа:
– это оператор Лапласа, то уравнение неразрывности для случая потенциального движения несжимаемой жидкости преобразуется в уравнение Лапласа:
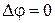 . (3.1г)
. (3.1г)
В случае установившегося движения газа при решении практических задач часто используется уравнение неразрывности в форме уравнения массового расхода:
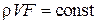 , (3.2)
, (3.2)
где F – площадь поперечного сечения трубки тока, или (при движении несжимаемой среды) в форме объемного расхода:
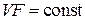 . (3.2а)
. (3.2а)
Формулы (3.2) и (3.2а) получаются элементарным образом при рассмотрении расхода сжимаемой и несжимаемой жидкости через поперечные сечения трубки тока.
 2015-03-22
2015-03-22 552
552







