Введем следующие обозначения: U – внутренняя энергия единицы массы жидкости; 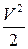 – ее кинетическая энергия. Тогда полная энергия рассматриваемой массы жидкости
– ее кинетическая энергия. Тогда полная энергия рассматриваемой массы жидкости 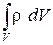 равна
равна 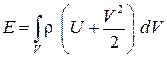 .
.
Применим закон сохранения энергии:
 Изменение энергии некоторой массы жидкости за некоторый промежуток времени равно работе всех сил, приложенных к данной массе жидкости (за данный промежуток времени), плюс/минус количество тепла, полученное за этот же промежуток времени вследствие теплопроводности, лучеиспускания или химических реакций.
Изменение энергии некоторой массы жидкости за некоторый промежуток времени равно работе всех сил, приложенных к данной массе жидкости (за данный промежуток времени), плюс/минус количество тепла, полученное за этот же промежуток времени вследствие теплопроводности, лучеиспускания или химических реакций.
Тогда изменение энергии в единицу времени запишем как
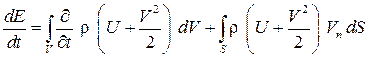 ,
,
где первое слагаемое представляет собой изменение энергии рассматриваемой массы в единицу времени; второе – изменение энергии данной массы за счет переменности ее объема, которое по теореме Остроградского–Гаусса можно записать следующим образом:
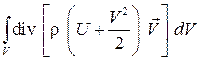 .
.
Тогда изменение энергии массы газа 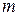 представим в виде
представим в виде
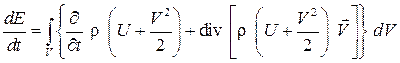 . (3.13)
. (3.13)
Изменение энергии некоторой массы газа может происходить за счет работы внешних сил и подвода или отвода тепла. Работа внешних по отношению к рассматриваемой системе сил складывается из трех составляющих:
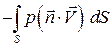 – работа сил давления в единицу времени;
– работа сил давления в единицу времени;
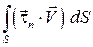 – работа сил трения в единицу времени;
– работа сил трения в единицу времени;
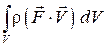 – работа массовых сил.
– работа массовых сил.
Тепло, подводимое или отводимое от выделенного объема, представим следующим образом: 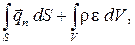 где
где 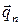 – вектор потока тепла, проходящего (уходящего) внутрь объема V в единицу времени через единицу поверхности;
– вектор потока тепла, проходящего (уходящего) внутрь объема V в единицу времени через единицу поверхности; 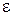 – количество тепла, выделяемое (поглощаемое) единицей массы в единицу времени (объемное выделение тепла, возможное, например, за счет химических реакций).
– количество тепла, выделяемое (поглощаемое) единицей массы в единицу времени (объемное выделение тепла, возможное, например, за счет химических реакций).
Тогда
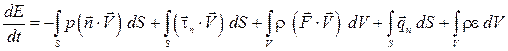 .
.
Преобразуем интегралы по поверхности в интегралы по объему:
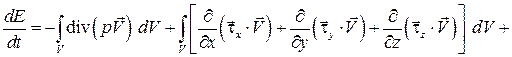
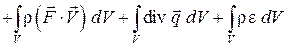 ;
;
воспользуемся выражением для изменения энергии данной массы (3.13) и после объединения интегралов, учитывая, что объем интегрирования произвольный, получим закон сохранения энергии в дифференциальной форме:
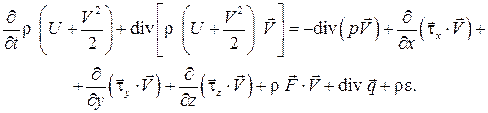 (3.14)
(3.14)
Преобразуем левую часть этого выражения следующим образом:
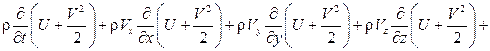
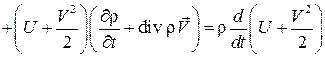 .
.
Тогда
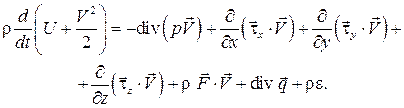 (3.15)
(3.15)
Воспользуемся уравнением, выражающим закон изменения количества движения вязкой жидкости в векторном виде:
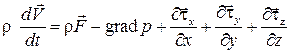 .
.
Умножим его скалярно на вектор скорости 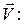
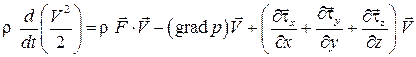 . (3.16)
. (3.16)
После подстановки уравнения (3.16) в уравнение (3.15) получаем
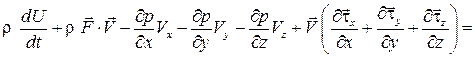
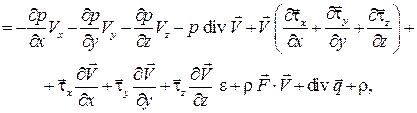
или после сокращений
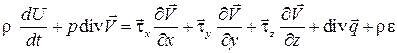 . (3.16а)
. (3.16а)
Из уравнения неразрывности (3.1б) получаем 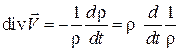 . Тогда из уравнения (3.16а) получаем
. Тогда из уравнения (3.16а) получаем 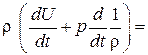
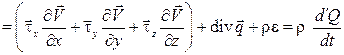 – уравнение энергии в виде 1-го закона термодинамики.
– уравнение энергии в виде 1-го закона термодинамики.
В этом уравнении 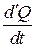 – количество тепла, получаемое единицей массы жидкости в единицу времени, в которое входит диссипативная функция
– количество тепла, получаемое единицей массы жидкости в единицу времени, в которое входит диссипативная функция 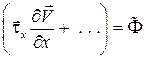 , представляющая собой количество тепла, выделяемого в данном объеме за счет работы сил трения. Все сообщенное количество тепла идет на увеличение внутренней энергии жидкости и на совершение ею механической работы.
, представляющая собой количество тепла, выделяемого в данном объеме за счет работы сил трения. Все сообщенное количество тепла идет на увеличение внутренней энергии жидкости и на совершение ею механической работы.
Если 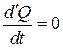 , то мы наблюдаем адиабатический процесс. Как следует из уравнения энергии, это возможно, если жидкость идеальная (нет сил трения), отсутствует теплопередача между частицами жидкости и объемное выделение тепла.
, то мы наблюдаем адиабатический процесс. Как следует из уравнения энергии, это возможно, если жидкость идеальная (нет сил трения), отсутствует теплопередача между частицами жидкости и объемное выделение тепла.
Представим уравнение энергии в другом виде, введя в рассмотрение функцию 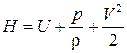 – теплосодержание единицы массы движущейся жидкости (
– теплосодержание единицы массы движущейся жидкости (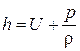 – теплосодержание единицы массы покоящейся жидкости). Добавим к левой и правой частям уравнения энергии (3.14) равенство
– теплосодержание единицы массы покоящейся жидкости). Добавим к левой и правой частям уравнения энергии (3.14) равенство 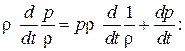
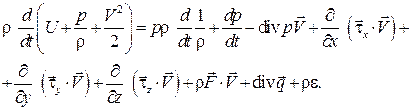
Преобразуем первые три слагаемые в правой части:
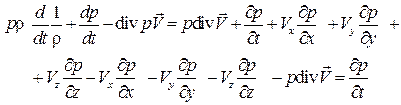
и получим следующее уравнение:
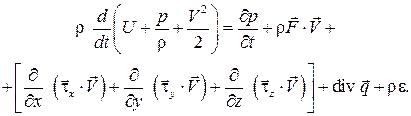 (3.17)
(3.17)
Из уравнения (3.17) следует, что при адиабатическом процессе (теплосодержание Н = const) должны выполняться следующие условия:
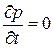 и
и 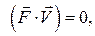
т. е. давление не должно зависеть от времени, а вектор массовых сил должен быть перпендикулярен вектору скорости или равен нулю. Так как в этом случае правая часть равенства обращается в нуль (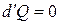 ), то
), то
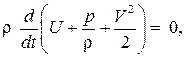
или в интегральном виде уравнение энергии будет выглядеть следующим образом: 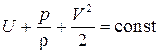 . Далее получим выражение для внутренней энергии.
. Далее получим выражение для внутренней энергии.
 2015-03-22
2015-03-22 1709
1709
