Внутренняя энергия и теплоемкость

Получим выражение для внутренней энергии и теплосодержания единицы массы жидкости.

Внутренняя энергия единицы массы U зависит от параметров состояния. Так как p, V, T связаны уравнением состояния, то независимыми переменными являются только какие-нибудь два из них, и можно считать: U = U (V, T), где .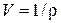

Отсюда полный дифференциал внутренней энергии равен

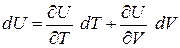. (3.18)

Чтобы иметь возможность проинтегрировать уравнение (3.18) и получить расчетную формулу для внутренней энергии, нужно определиться с частными производным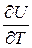и и .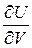

Согласно первому закону термодинамики

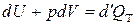, (3.18а)

где 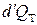– количество тепла, получаемое единицей массы жидкости за время 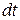( 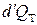не является полным дифференциалом). Исключив из выражения (3.18) и (3.18а) дифференциал 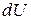, имеем следующее:

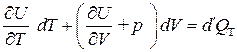. (3.19)

Введем понятие удельной теплоемкости с как физической величины, численно равной количеству тепла, которое необходимо сообщить (отнять) единице массы жидкости, чтобы изменить ее температуру на 1 К:

.

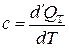Если тепло подводить к единице массы жидкости, сохраняя постоянным объем, то удельную теплоемкость называют теплоемкостью при постоянном объеме – 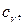если тепло подводить при p = const – то теплоемкостью при постоянном давлении – 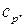В условиях, далеких от сжижения газов, теплоемкость зависит от температуры газа и почти не зависит от давления. Тогда выражение для 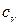имеет вид

.

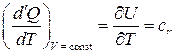Таким образом, определился первый коэффициент уравнения (3.18). Для определения 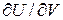воспользуемся выражением для дифференциала энтропии. Энтропия – это функция, которая определяется следующим дифференциальным уравнением:

.

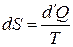Процессы, протекающие без теплообмена и при отсутствии потерь механической энергии, т. е. при S = const называются изоэнтропическими. С учетом уравнения (3.19) имеем следующее:

.

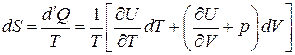Так как dS – полный дифференциал, то накрест взятые частные производные от коэффициентов при dT и dV должны быть равны между собой. То есть

.

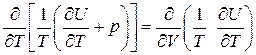После дифференцирования 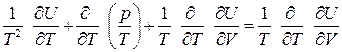и сокращения получаем 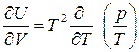. Для дальнейшего преобразования воспользуемся уравнением состояния. Для идеальных газов 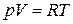. Отсюда 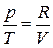, т. е. 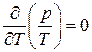и 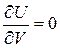. Для реальных газов, подчиняющихся уравнению состояния Ван-дер-Ваальса

.

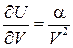Теперь можно получить выражения для внутренней энергии (для идеального и реального газа):

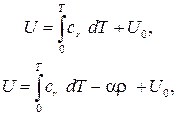(3.20)

где 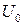– внутренняя энергия жидкости при температуре Т = 0 К; для идеального газа .

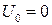Установим связь между теплоемкостям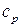и и 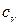. Если уравнение состояния идеального газа разрешить относительно V, то получим

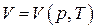и .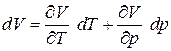

Из выражения (3.19) можно записать следующее:

.

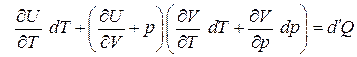Тогда при p = const

.

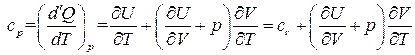Для идеальных газов 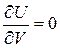; из уравнения состояния 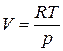и 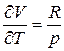. Отсюда 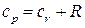. Отношение удельных теплоемкостей обозначим 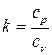, тогд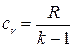а , а .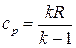

Для реальных газов 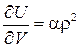, 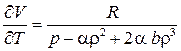и .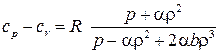

С учетом полученных зависимостей выражение для теплосодержания единицы массы неподвижного идеального газа (энтальпии) следующие:

.

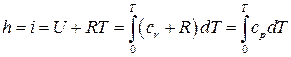Считая, что 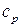не зависит от температуры, выражение для энтальпии можно представить следующим образом:

.

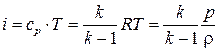Получим выражение для энтропии идеального газа. Так как 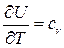, 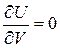и 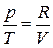, то, считая R и 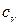постоянными, выражение для дифференциала энтропии можно привести к виду

,

,

.

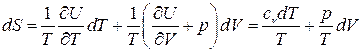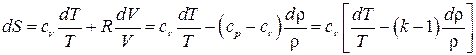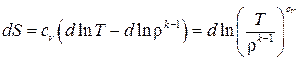После интегрирования получаем следующее:

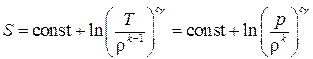. (3.21)

Если рассматривается изоэнтропический или адиабатический процесс, для которого характерно постоянство энтропии (S = const), то и второе слагаемое в выражении (3.21) должно быть неизменным, т. е.

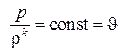. (3.22)

Выражение (3.22) носит название адиабаты Пуассона, и в соответствии с этим показатель степени в этом выражении k называют показателем адиабаты. Соотношение (3.22) имеет место в частице, и 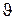может изменяться от частицы к частице. При установившемся движении 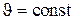на линии тока.

Предположение о постоянстве 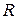и 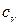, при котором получено соотношение (3.22), справедливо в определенном диапазоне температур, зависящем от физических свойств газа. Величина показателя адиабаты 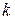зависит от структуры молекул газа: для одноатомных газов 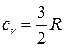и 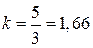; для двухатомных, к которым можно отнести и воздух, 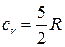и 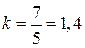; для трехатомных .

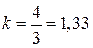Интегралы дифференциальных уравнений Эйлера

В общем виде дифференциальные уравнения движения Эйлера не интегрируются. Их интегралы можно найти только для некоторых частных случаев. Рассмотрим порядок нахождения интегралов:

1) для потенциального неустановившегося движения;

2) для установившегося непотенциального движения сжимаемого газа.