2015-03-22
3068
При установившемся движении траектории и линии тока совпадают, и параметры течения являются функциями только координат. Считая движение баротропным, т. е.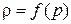 
, уравнения Эйлера запишем в виде
, 
, 
.
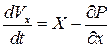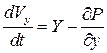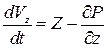После умножения каждого уравнения на соответствующее приращение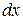 
, 
, 
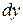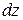и их суммирования получаем
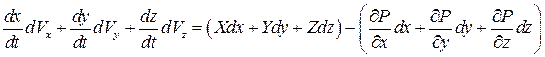. (3.27)
Так как на линии тока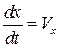 
, 
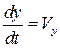и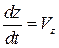 
, левая часть уравнения (3.27) представляет собой полный дифференциал 
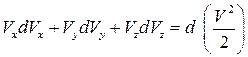. Следовательно, и правая часть уравнения (3.27) должна быть суммой полных дифференциалов:
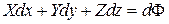и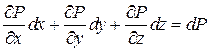 
.
Тогда уравнение (3.27) можно переписать в виде
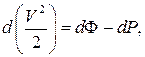или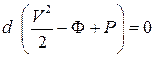 
. (3.28)
Взяв неопределенный интеграл от выражения (3.28), получим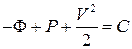 
. С учетом выражения для функции давления
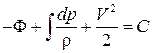. (3.29)
Полученное выражение есть интеграл уравнений Эйлера для установившегося движения сжимаемого газа, который носит название интеграла Бернулли. Интеграл Бернулли (3.29) тождественен по записи интегралу Эйлера–Бернулли. Однако разница здесь существенна и заключается в том, что произвольная постоянная в интеграле Бернулли (3.29) есть постоянная только вдоль линии тока.
|
|
|
Для несжимаемой жидкости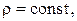 
и уравнение (3.29) перепишется в упрощенном виде: 
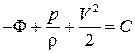. Пренебрегая массовыми силами (для газа), получаем уравнение Бернулли в виде
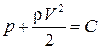. (3.30)
Уравнение Бернулли (3.30) показывает, что при установившемся движении несжимаемой жидкости полный напор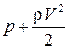 
вдоль линии тока остается неизменным.
Для сжимаемого газа (без учета массовых сил) уравнение (3.29) имеет вид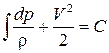 
. Для изоэнтропического течения 
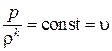. Отсюда 
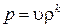, и дифференциал 
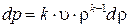, а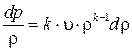 
. Поэтому
.
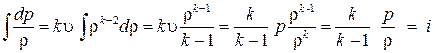Уравнение Бернулли для сжимаемого газа будет иметь вид
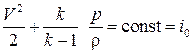, (3.31)
где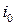 
– полная энтальпия, включающая энтальпию и кинетическую энергию единицы массы движущегося газа. Уравнение Бернулли есть уравнение энергии для изоэнтропического течения сжимаемого (или несжимаемого) газа.
Выражения для полной энтальпии можно записать через параметры заторможенного газа: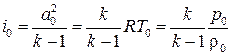 
. Другие формы представления энтальпии будут приведены далее.
Сравнивая интегралы Лагранжа и Бернулли, можно заметить, что интеграл Лагранжа в некотором смысле более общий, так как годится и для неустановившихся движений. Однако он менее общий в том смысле, что требует безвихревого движения и полной баротропности во всем пространстве движущейся жидкости.
Примеры на применение уравнения Бернулли
Рассмотрим порядок применения уравнения Бернулли для нахождения установившегося течения газа через малое отверстие, для объяснения возникновения подъемной силы и оценки влияния сжимаемости.
