Метод малых возмущений

Степень возмущения потока вблизи тела определяется относительной толщиной тела и его ориентацией в пространстве. Рассмотрим основные положения метода малых возмущений на примере обтекания тонкого профиля под малым углом атаки 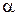. Поток около такого профиля мало отличается от плоскопараллельного невозмущенного потока, имеющего скорость 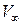. 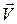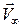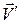Тогда представим скорость около профиля как сумму векторов и , где 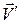– скорость возмущения. На этом основании составляющие скорости 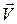вблизи профиля равны (ось ОX направлена вдоль вектора ):

,

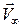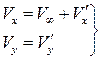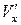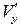где и – составляющие скорости возмущения (, ).

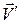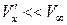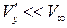Утверждение о малости возмущений справедливо везде, за исключением критической точки. В ее окрестности скорость потока равна нулю, т. е. 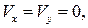и составляющая скорости возмущения 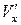равна по величине 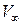и противоположна ей. Предположим, что малому возмущению скорости соответствуют также малые изменения давления, плотности и температуры.

Сущность метода малых возмущений (метода линеаризации) заключается в том, что во всех формулах удерживаются только члены первого порядка малости (вторыми и более высокими степенями малых величин 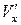, 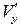и т. д. можно пренебречь).

Произведем линеаризацию уравнения (5.5). Рассмотрим вначале квадрат скорости:

.

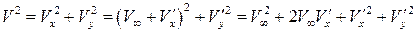Оставляя только величины не ниже первого порядка малости, получаем 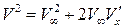. Тогда выражение для скорости потока 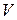будет иметь вид

.

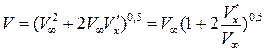Так как по условию 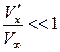, то используем известный из математики прием приближенного вычисления подобного выражения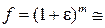 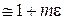(при условии 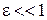). Таким образом, окончательно получаем

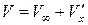. (5.6)

Аналогичные преобразования проведем с выражением для скорости звука:

.

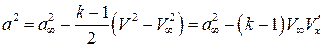То есть 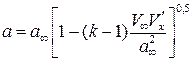. В окончательном виде

.

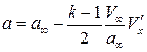Сравним между собой числа Маха потока около профиля 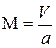и в невозмущенном потоке 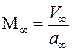, используя положения метода малых возмущений:

.

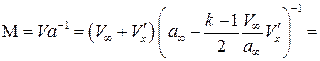
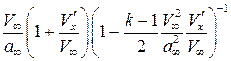Применив уже использовавшийся метод приближенного вычисления, ввиду малости дроби во второй скобке, получим

.

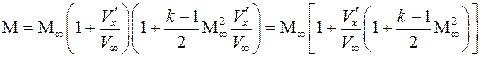Найдем давление в возмущенном потоке. Из уравнения Бернулли (3.30) 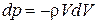. Интегрируем в пределах для давления от 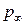до 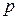и для скорости от 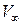до 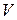. Тогда .

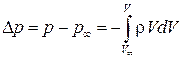Произведение 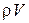(удельный расход через единицу площади) для невозмущенного потока равно 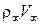, а для возмущенного потока равно 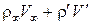. Произведем замену 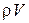под интегралом на его среднее значение:

,

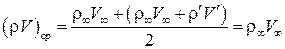и после интегрирования получим

.

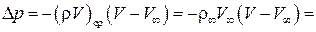
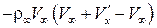В результате, окончательно получаем

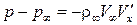. (5.7)

Выражение (5.7) представляет собой линеаризованное уравнение Бернулли.

Для линеаризации основного дифференциального уравнения газовой динамики (5.5) заменим в нем 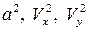и 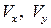через их линеаризованные выражения. Тогда с принятой точностью

.

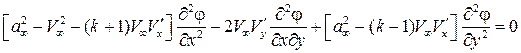Определим порядок величины вторых производных от потенциала скорости. Так 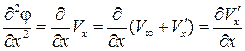, т. е. 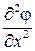имеет первый порядок малости. То же самое можно сказать и о других производных, входящих в линеаризуемое уравнение. Отбрасывая члены второго порядка малости, после деления на 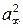получаем

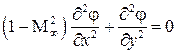, (5.8)

т. е. линейное дифференциальное уравнение.

Рассмотренный метод упрощения и преобразования исходного нелинейного дифференциального уравнения (5.5) называют методом линеаризации, а сам поток, описываемый уравнением (5.8), – линеаризованным потоком.

В случае трехмерного потока газа линеаризованное уравнение движения можно записать по аналогии с уравнением (5.8) в виде

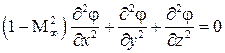. (5.8а)

Уравнения (5.8) и (5.8а) справедливы как для дозвуковых (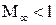), так и для сверхзвуковых (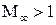) скоростей. Однако методы их решения различны и будут рассмотрены далее и для дозвуковых, и для сверхзвуковых скоростей.