2015-03-22
520
Пусть газ движется в плоскости чертежа слева направо со сверхзвуковой скоростью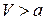 
.
В каждой точке плоскости XОY можно провести два направления линий возмущения (линий Маха). При переходе от одной точки к другой направление линий возмущения может изменяться, так как значения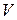 
и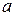 
в разных точках плоскости XОY в общем случае различны. Имея это в виду, найдем в плоскости такую кривую y = y (x), в каждой точке которой направление касательной совпадало бы с направлением одной из линий возмущения для данной точки (рис. 5.3). Кривую, обладающую таким свойством, называют характеристикой.
Из рис. 5.3 следует, что
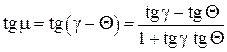. (5.11)
|
Для линии возмущений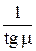 
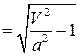, из треугольника скоростей 
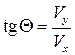, а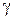 
есть угол наклона касательной к кривой y = y (x), для которого 
.
|
|
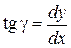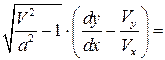
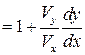. Возведя обе части равенства в квадрат, после преобразований получим квадратное уравнение относительно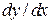 
,
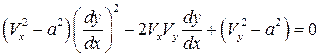корни которого равны
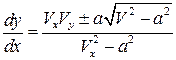. (5.12)
Выражение (5.12) представляет собой дифференциальное уравнение характеристик в плоскости потока. Анализ уравнения (5.12) позволяет установить следующее:
1. Для сверхзвукового потока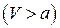 
имеются два вещественных различных корня. Через каждую точку плоскости можно провести два элемента характеристик, а вся плоскость может быть покрыта двумя семействами характеристик. Уравнение (5.12) является уравнением гиперболического типа.
Для определенности интегральные кривые y = y (x), соответствующие уравнению (5.12) со знаком «+», называют характеристиками первого семейства, а соответствующие уравнению со знаком «–» – характеристиками второго семейства.
2. Для звукового потока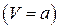 
имеется один вещественный корень и одно семейство характеристик; уравнение (5.12) является уравнением параболического типа.
3. Если поток газа дозвуковой (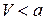
), то вещественных корней и характеристик нет, уравнение (5.12) является уравнением эллиптического типа.
