2015-03-22
867
Глава 5
ТЕЧЕНИЯ ГАЗА
В пространстве движущегося газа по большому счету, за исключением некоторых достаточно ограниченных областей (пограничный слой, след за телом и др.), имеет место безвихревое, или потенциальное течение. Выясним, при каком условии течение можно считать потенциальным, т. е. при каком условии в потоке будут отсутствовать вихри.
Рассмотрим какую-нибудь линию тока аА (рис. 5.1). Проведем касательную к линии тока в точке а (совпадает с направлением вектора скорости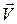 
) и внутреннюю нормаль n. Уравнение движения в проекции на нормаль n запишется следующим образом:
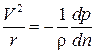, (5.1)
где r = Оа – радиус кривизны линии тока;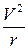 
– центростремительное ускорение. Вдоль линии тока полная удельная энергия и энтропия не изменяют своей величины, т. е. 
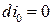и dS = 0.
Допустим, что при переходе от одной линии тока аА к другой bВ, расположенной на расстоянии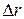 
от аА, полная удельная энергия 
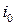и энтропия газа 
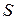изменяются. То есть
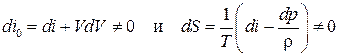. (5.2)
Исключив из уравнений (5.2)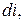 
получим 
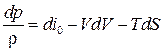. Тогда 
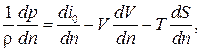и после подстановки в уравнение движения (5.1) имеем следующее:
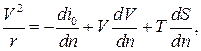или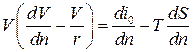 
.
Выражение в скобках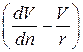 
есть не что иное, как удвоенная угловая скорость 
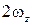. Из условия потенциальности (вращательное движение отсутствует) 
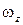= 0, следовательно, 
.
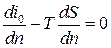Это равенство в общем случае выполняется, есл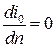и 
и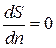 
.
Случай выполнения этого равенства пр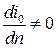и 
и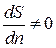 
не представляет интереса, так как он соответствует движению с линиями тока в виде либо концентрических окружностей, либо параллельных прямых.
Таким образом, поток газа можно считать потенциальным, если полная удельная энергия и энтропия при переходе от одной линии тока к другой не изменяются.
Основное дифференциальное уравнение плоского
потенциального потока газа
Рассмотрим плоский потенциальный газовый поток (установившееся течение). Уравнение неразрывности для такого течения имеет вид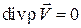 
, которое для плоского потока запишется как 
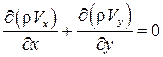. Проведя дифференцирование в этом уравнении, получаем
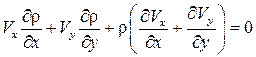. (5.3)
Выразим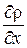 
и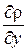 
через проекции скорост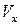и 
и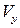 
. Считая движение баротропным 
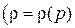, где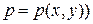 
, можно записать, что
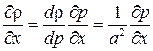и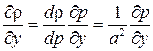 
.
Заменим в этих выражениях 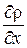и 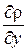через уравнения Эйлера (3.6) и (3.7) с учетом малости массовых сил, т. е. 
, 
,
.
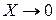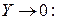
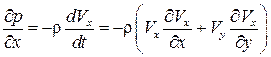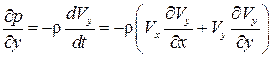Тогда имеем следующее:
,
.
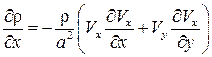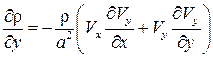Полученные выражения подставим в уравнение (5.3) и приведем его к следующему виду:
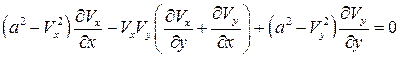. (5.4)
Учтем, что для потенциального потока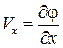 
, 
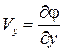, и уравнение (5.3) примет вид
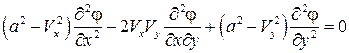. (5.5)
Уравнение (5.5) представляет собой основное дифференциальное уравнение газовой динамики для плоского потенциального установившегося газового потока. Это нелинейное дифференциальное уравнение второго порядка в частных производных относительно неизвестной функции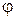 
. Однако коэффициенты при вторых производных в явном виде от координат х и y не зависят, поэтому уравнение (5.5) называют квазилинейным дифференциальным уравнением.
Для решения уравнения применяют два метода:
1) метод малых возмущений (метод линеаризации), который широко используется при исследовании обтекания тонких тел при малых углах атаки как в дозвуковом, так и в сверхзвуковом потоке и позволяет получить решение в аналитическом виде;
2) метод характеристик – численный метод, который применяется для определения поля скоростей в сверхзвуковом потоке.
