2015-03-22
629
Рассмотрим установившийся плоский пограничный слой. Выделим в пограничном слое малый объем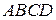 
(рис. 7.5). Применим к данному объему теорему об изменении количества движения. Вычислим изменение количества движения в направлении оси ОХ за промежуток времени 
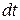. Через грань 
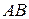в выделенный объем втекает масса 
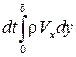, а через грань 
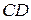вытекает масса 
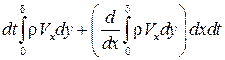. Разность между ними равна 
.
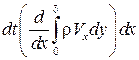На основании условия неразрывности такая же масса должна втекать в объем 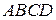через верхнюю границу 
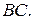Эта масса вносит количество движения 
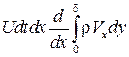, где U – скорость потока на внешней границе пограничного слоя. Найдем изменение количества движения жидкости в выделенном объеме. Количество движения, вносимое через грань 
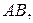равно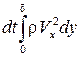 
, а уносимое через – 
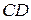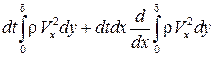. Тогда полное изменение количества движения в объеме 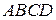за время 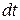равно
.
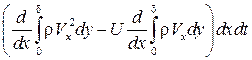Силы давления, действующие на грани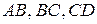 
, единичной протяженностью в направлении, перпендикулярном плоскости рисунка (рис. 7.5), в проекции на ось ОХ равны
, 
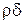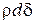и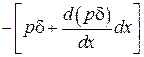 
.
Сумма проекций сил давления равна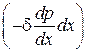 
, а импульс сил 
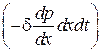. Кроме того, на грань 
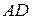действует сила трения, направленная против потока и оси ОХ:
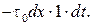
Приравняв изменение количества движения жидкости в объеме 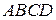суммарному импульсу от сил давления и трения, получаем
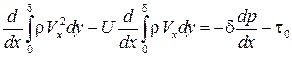. (7.8)
Соотношение (7.8) называют интегральным соотношением пограничного слоя. Оно пригодно для изучения как ламинарного, так и турбулентного пограничных слоев. При использовании этого соотношения для решения задач необходимы два дополнительных уравнения (неизвестные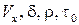 
):
1. Закон распределения скорости по поперечному сечению пограничного слоя, который можно задать приближенно аппроксимирующей функцией.
2. Зависимость напряжения трения от изменения скорости по нормали к поверхности. Например, для ламинарного пограничного слоя можно использовать формулу Ньютона (1.1).
В результате подстановки выражений для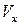 
и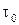 
получаем обыкновенное дифференциальное уравнение, позволяющее определить толщину пограничного слоя.
Интегральное соотношение можно привести и к другому виду. Из уравнения Эйлера–Бернулли (см. гл. 3) запишем следующее:
.
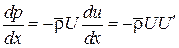Так как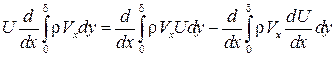 
, то после подстановок в выражение (7.8) интегральное соотношение будет иметь вид
.
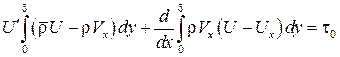Первый интеграл, исходя из сопоставления с выражением для толщины вытеснения, можно записать как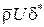 
, а второй – через толщину потери импульса: 
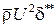. Таким образом, 
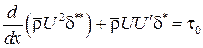. Считая 
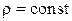, получим
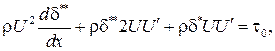
или
.
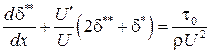Введя в рассмотрение формпараметр, представляющий собой отношение толщины вытеснения к толщине потери импульса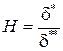 
, получим
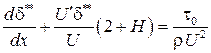. (7.9)
В таком виде интегральное соотношение более удобно для расчета пограничного слоя около криволинейных поверхностей.
