2015-03-22
683
Для установившегося плоскопараллельного потока сжимаемого газа в уравнениях Навье–Стокса (7.2) произведем оценку порядка величин членов этих уравнений для пограничного слоя несжимаемой жидкости. Тогда первое уравнение системы
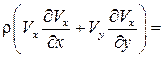
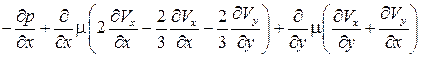
после анализа порядков величин его членов упрощается и запишется следующим образом:
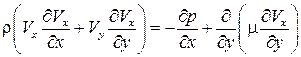. (7.7)
Вторым уравнением системы (7.2) так же, как и для несжимаемой жидкости, можно пренебречь. Из него также следует, что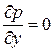 
, т. е. вновь возможна заме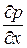на 
на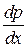 
.
Уравнение неразрывности для установившегося движения сжимаемой жидкости (3.1а) для плоского случая запишем как
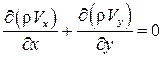. (7.7а)
Так как в уравнении (7.7) коэффициент вязкости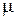 
является функцией температуры, то к записанным двум уравнения необходимо добавить уравнение энергии. После его преобразования с учетом малости членов получаем
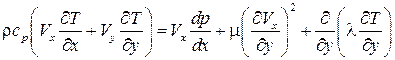, (7.7б)
где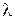 
– коэффициент теплопроводности 
.
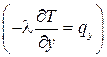Таким образом, для установившегося движения сжимаемого газа в пограничном слое необходимо решать систему трех уравнений (7.7). Основные неизвестные в этой системе уравнений –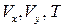 
. Так как 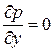, то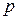 
можно считать известным. С помощью уравнения состояния плотность определится как 
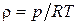, а коэффициенты вязкости 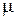и теплопроводности 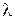можно считать известными функциями температуры.
Решение дифференциальных уравнений пограничного слоя, как для сжимаемой, так и для несжимаемой жидкости, достаточно сложная процедура даже для простейших тел. В связи с этим используют приближенные методы решения задач пограничного слоя, основанные на рассмотрении интегрального соотношения, являющегося математическим выражением теоремы об изменении количества движения.
