Для области тонкого пограничного слоя, в котором собственно и проявляются силы трения, Л. Прандтль предложил особый метод упрощения уравнений движения (7.3), основанный на сравнении порядка величины членов уравнения и отбрасывания членов высшего порядка малости.
 Пусть поток движется вдоль твердой прямолинейной границы в направлении оси ОХ (рис. 7.4). Вдоль этой границы образуется пограничный слой, толщина которого
Пусть поток движется вдоль твердой прямолинейной границы в направлении оси ОХ (рис. 7.4). Вдоль этой границы образуется пограничный слой, толщина которого 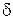 . Рассмотрим плоский пограничный слой в установившемся потоке несжимаемой жидкости (
. Рассмотрим плоский пограничный слой в установившемся потоке несжимаемой жидкости (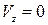 , скорость течения не зависит от времени, плотность постоянная). Массовыми силами для газа можно пренебречь (
, скорость течения не зависит от времени, плотность постоянная). Массовыми силами для газа можно пренебречь (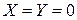 ). С учетом принятых допущений запишем уравнения Навье–Стокса следующим образом:
). С учетом принятых допущений запишем уравнения Навье–Стокса следующим образом:
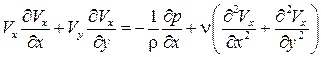 , (7.4)
, (7.4)
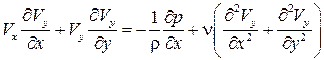 , (7.4а)
, (7.4а)
и уравнение неразрывности 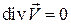 в виде
в виде
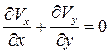 . (7.4б)
. (7.4б)
Эта система уравнений полностью описывает движение вязкой жидкости в пределах пограничного слоя в рамках настоящей задачи.
Оценим порядок входящих в эти уравнения членов, имея в виду, что 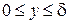 , т. е.
, т. е. 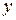 имеет порядок толщины пограничного слоя
имеет порядок толщины пограничного слоя 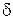 (
(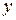 ~
~ 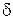 ) и является малой величиной по сравнению с характерным размером обтекаемой поверхности, например, его длиной
) и является малой величиной по сравнению с характерным размером обтекаемой поверхности, например, его длиной 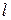
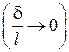 . Скорость в пределах пограничного слоя
. Скорость в пределах пограничного слоя 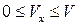 (
(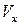 ~
~ 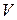 ), продольная координата
), продольная координата 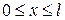 , т. е.
, т. е. 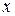 ~
~ 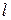 .
.
Тогда приращение скорости 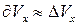 имеет порядок величины скорости во внешнем потоке
имеет порядок величины скорости во внешнем потоке 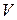 . Установим порядок величины производных, входящих в уравнения (7.4):
. Установим порядок величины производных, входящих в уравнения (7.4):
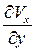 ~
~ 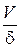 ;
; 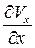 ~
~ 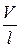 ;
; 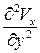 ~
~ 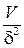 ;
; 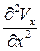 ~
~ 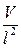 .
.
С учетом уравнения неразрывности (7.4б) 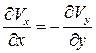 ~
~ 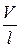 . Поскольку
. Поскольку 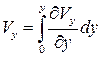 , то
, то 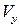 ~
~ 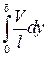 ~
~ 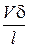 ,
, 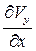 ~
~ 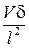 ,
, 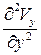 ~
~ 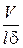 . Записав порядки величин членов уравнения (7.4), сравним их:
. Записав порядки величин членов уравнения (7.4), сравним их:
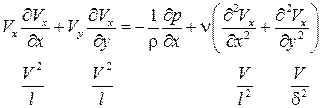 .
.
Сравнение показывает, что оба слагаемых левой части уравнения (инерционные члены) имеют один и тот же порядок малости 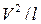 . Вязкие члены (в скобках правой части) имеют разный порядок, причем первое слагаемое существенно меньше второго: отношение первого ко второму равно
. Вязкие члены (в скобках правой части) имеют разный порядок, причем первое слагаемое существенно меньше второго: отношение первого ко второму равно 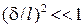 . Поэтому первым слагаемым можно пренебречь, и уравнение (7.4) запишется в несколько упрощенном виде:
. Поэтому первым слагаемым можно пренебречь, и уравнение (7.4) запишется в несколько упрощенном виде:
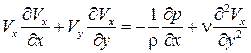 . (7.5)
. (7.5)
Внутри пограничного слоя силы вязкости и силы инерции имеют одинаковый порядок, т. е. их отношение должно быть равным единице. Тогда из уравнения (7.5), записав инерционный и вязкий члены через их порядки, получаем, что их отношение равно 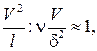 и отсюда
и отсюда 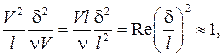 откуда получается вполне очевидное соотношение:
откуда получается вполне очевидное соотношение: 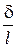 ~
~ 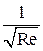 .
.
Проведя подобный анализ членов второго уравнения (7.4а), приходим к аналогичной выражению (7.5) упрощенной записи:
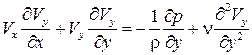 .
.
Инерционные члены этого уравнения имеют порядок 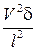 и относятся к инерционным членам первого уравнения как
и относятся к инерционным членам первого уравнения как 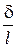 (малая величина). Точно в таком же отношении друг к другу находятся и вязкие члены. Следовательно, решая задачу с использованием обоих уравнений, мы приходим к выводу, что наибольший вклад в конечный результат дает уравнение (7.5). Очевидно, что вклад второго уравнения не превышает указанного отношения, т. е.
(малая величина). Точно в таком же отношении друг к другу находятся и вязкие члены. Следовательно, решая задачу с использованием обоих уравнений, мы приходим к выводу, что наибольший вклад в конечный результат дает уравнение (7.5). Очевидно, что вклад второго уравнения не превышает указанного отношения, т. е. 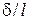 . Поэтому инерционными и вязкими членами второго уравнения можно пренебречь и в задаче исследования течения в пограничном слое вообще не учитывать. Тогда из второго уравнения системы с достаточной точностью можно записать следующее:
. Поэтому инерционными и вязкими членами второго уравнения можно пренебречь и в задаче исследования течения в пограничном слое вообще не учитывать. Тогда из второго уравнения системы с достаточной точностью можно записать следующее:
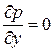 .
.
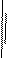 То есть, давление внутри пограничного слоя не меняется вдоль нормали к контуру тела и равняется давлению на внешней границе пограничного слоя.
То есть, давление внутри пограничного слоя не меняется вдоль нормали к контуру тела и равняется давлению на внешней границе пограничного слоя.
Это один из главных выводов, полученных в результате упрощения исходной системы уравнений.
Таким образом, распределение давления вдоль поверхности тела совпадает с распределением давления на внешней границе пограничного слоя, которое можно найти, решая задачу обтекания данного тела невязким (потенциальным) потоком.
Так как 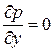 , то
, то 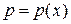 и
и 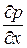 =
= 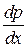 . В результате упрощений получаем систему уравнений, описывающих движение вязкой жидкости в пределах пограничного слоя:
. В результате упрощений получаем систему уравнений, описывающих движение вязкой жидкости в пределах пограничного слоя:
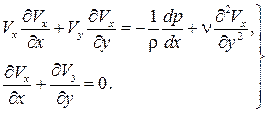 (7.6)
(7.6)
Система уравнений (7.6) интегрируется при следующих граничных условиях:
1) при 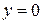 – на внутренней границе пограничного слоя (на стенке)
– на внутренней границе пограничного слоя (на стенке) 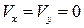 ;
;
2) при 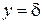 – на внешней границе пограничного слоя скорость течения равна скорости потенциального потока:
– на внешней границе пограничного слоя скорость течения равна скорости потенциального потока: 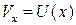 .
.
 2015-03-22
2015-03-22 1094
1094








