2015-03-22
679
Решение задачи об обтекании плоской пластинки в теории сопротивления играет большую роль. Найденная для пластинки зависимость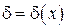 
и величина коэффициента сопротивления трения могут быть использованы при приближенных расчетах других удобообтекаемых тел.
Задача расчета пограничного слоя в несжимаемой среде сводится к определению закона изменения толщины пограничного слоя, т. е. 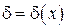, и силы сопротивления трения 
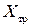при условии, что известны скорость 
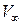, величина коэффициента кинематической вязкости и хорда пластинки 
.
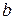Для плоской пластинки (рис. 7.6) скорость потенциального течения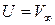 
, градиент давления вдоль пластинки 
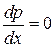(пластинка – тело с нулевым градиентом давления вдоль ее хорды). С учетом вышеизложенного интегральное соотношение (7.8) приобретает вид
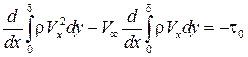. (7.10)
Для решения задачи о пограничном слое введем дополнительно еще два соотношения:
1) закон распределения скорости по толщине пограничного слоя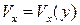 
;
2) уравнение, связывающее касательное напряжение на стенке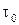 
с толщиной пограничного слоя 
.
|
|
|
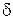Вид этих соотношений зависит от состояния пограничного слоя.
