Динамическое программирование

В теории управления для оптимизации функционалов при наличии ограничений на векторы управления и состояния применяют принцип максимума и метод динамического программирования, разработанные в 1956…1957 годах российским и американским математиками Л.С.Понтрягиным и Р. Беллманом на основе классических методов вариационного исчисления Эйлера, Лагранжа.

Динамическое программирование является методом решения задач оптимального управления для замкнутых областей. Оно отличается как от классических вариационных методов, так и от принципа максимума, хотя и находится с ним в тесной связи.

В основе динамического программирования лежит следующий «принцип оптимальности», предложенный Р. Беллманом в качестве гипотезы: оптимальное поведение обладает тем свойством, что каковы бы ни были первоначальное состояние и решение (управление) и начальный момент, последующие решения (управления) должны составлять оптимальное поведение относительно состояния, получившегося в результате первого решения.

Доказательства этот принцип, по существу, не требует. Ведь если какой-то участок траектории (рис. 9.16) можно улучшить, оставляя неподвижными его концы (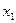 и 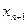), то и вся траектория не может быть оптимальной, так как траектория х ₁, …, х_i,..., 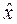,...., х_{n +1} окажется лучше.

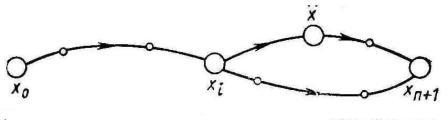
Рис. 9.16. К пояснению принципа оптимальности

На основании принципа оптимальности исходная задача об оптимальном попадании в состояние х_{n +1} из заданного состояния х ₀ может быть погружена в класс задач о попадании в состояние х_{n +1} из любого допустимого промежуточного состояния. На первый взгляд замена конкретной задачи целым классом задач того же типа сильно усложняет решение. В действительности, как это будет показано ниже, это не совсем так.

Следует иметь в виду, что теория динамического программирования разрабатывалась Р. Беллманом для более обширного класса процессов, чем процессы, описываемые системами обыкновенных дифференциальных уравнений. Поэтому Р. Беллман и опирался на столь общий принцип, как принцип оптимальности. В столь общей форме, как высказанная выше, принцип оптимальности не доказан, но для систем, описываемых дифференциальными уравнениями, справедливость его следует из того простого факта, что каждый отрезок экстремали есть тоже экстремаль и всякий участок оптимального управления также является оптимальным управлением.

Исходя из принципа оптимальности, Р. Беллман вывел дифференциальное уравнение в частных производных, позволяющее определить кривые, на которых достигается экстремум.

Рассмотрим автономную систему, движение которой описывается уравнениями

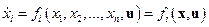, i =1: n, (9.49) (9.17)

где х_i — фазовые координаты системы, а u — функция управления, принимающая значения в некоторой допустимой области.

Пусть требуется для системы (9.49) найти такое допустимое управление, что при движении системы из заданной начальной точки x_i (t ₀), i = l, 2,..., n в начало координат достигается минимум следующего функционала:

J (u) = 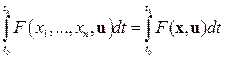(9.50) (9.18)

Введем в рассмотрение функцию

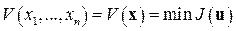, (9.51) (9.19)

называемую функцией Беллмана, предполагая, что она всюду, за исключением концов фазовой траектории, имеет непрерывные частные производные 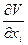; i = 1: n.

Тогда оптимальное управление u, доставляющее минимум функционалу (9.50), должно удовлетворять следующему уравнению:

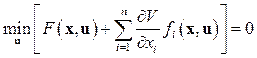. (9.52) (9.20)

В уравнение Беллмана (9.52), помимо неизвестной функции V, входит еще и неизвестная функция управления u. Используя требование минимизации выражения, стоящего в прямых скобках уравнения (9.52), последнее можно свести к следующей теме:

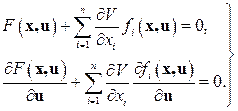(9.53) (9.21)

Одно из этих уравнений можно использовать для исключения величины u. При этом управление u будет выражаться через x и :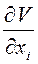

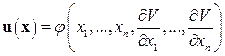. (9.54) (9.22)

Может оказаться, что управление u (x), найденное по (9.54), выходит за допустимые пределы. Тогда пользуются приемом ограничения управления по следующему правилу:

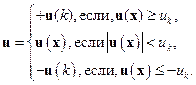
Однако использование этого приема требует известной осторожности, так как при этом траектория движения системы (9.49) разбивается на части, в каждой из которых ищутся различные аналитические выражения для функции V (x). Важно, чтобы при этом функция V (x) получалась непрерывной по x вдоль всей траектории движения. В противном случае уже нельзя будет утверждать, что найденное управление минимизирует исходный функционал (9.50).

Таким образом, если бы нам удалось найти функцию Беллмана, то оптимальное управление однозначно определилось через координаты управляемой системы.

В этом состоит конструктивная ценность метода динамического программирования. Однако лишь для очень небольшого числа задач можно указать вид функции V (x). Более того, предположение о дифференцируемости ее, как правило, не вытекает из постановки задач, и проверить его по уравнениям движения невозможно.

В связи с этим после решения оптимальной задачи необходимо проверить, является ли функция V (x) непрерывно дифференцируемой.

Следует, разумеется, иметь в виду, "что решение "уравнения в частных производных является гораздо более сложной задачей, чем интегрирование обыкновенных дифференциальных уравнений классического вариационного исчисления или принципа максимума. Поэтому значение динамического программирования заключается не столько в том, что оно позволяет решать задачи оптимизации в конечном виде (хотя некоторые технические задачи были решены именно этим методом), сколько в том, что динамическое программирование лежит в основе ряда численных алгоритмов решения задач оптимизации.

Общая идея приближенных алгоритмов, основанных на принципе оптимальности, заключается в том, что весь интервал, на котором нужно оптимизировать процесс, делят на такое число малых интервалов, чтобы решение задачи оптимизации на этом малом интервале было уже несложным. После этого решение задачи начинается «с конца». Как было указано выше согласно принципу оптимальности, оптимальное управление на последнем шаге не зависит от того, каким было управление на предыдущих шагах. На последнем шаге управление должно быть, во-первых, оптимальным для условий данного (и только данного) шага и, во-вторых, приводить в заданную конечную точку.

Однако для выбора управления на последнем шаге нужно знать, чем кончился предпоследний. Это даст начальное условие для последнего шага. Поскольку мы его не знаем, будем делать разные предположения об исходе предпоследнего шага и для каждого из этих предположений вычислять оптимальное управление и значение функционала на последнем шаге. После этого переходим к выбору управления на предпоследнем шаге, причем его выбираем так, чтобы оно совместно с уже выбранным управлением на последнем шаге обеспечивало экстремум функционала на двух последних шагах. Таким образом, процесс динамического программирования развивается в обратном по времени направлении — от конца к началу — до тех пор, пока не доходит до заданной начальной точки.

Характерные особенности алгоритмов динамического программирования удобно рассматривать на примере дискретной задачи. Представим себе прямоугольное поле из m·n клеток: m — по горизонтали и n — по вертикали. На рис. 9.17 для наглядности показано поле при m = 5 и n = 4. Пусть для каждой клетки задана «стоимость» перехода в любую клетку соседнего справа столбца. Требуется найти оптимальную по стоимости траекторию перехода из заданной клетки крайнего левого столбца в заданную клетку крайнего правого столбца. Если искать оптимальный путь простым перебором, то придется сравнивать между собой 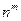возможных путей, а это очень большое число. При больших n и m прямой перебор нереален.

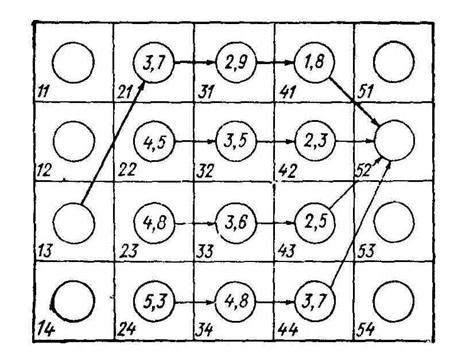
Рис. 9.17. Иллюстрация оптимальной траектории

Рассмотрим теперь, что может в этой ситуации дать динамическое программирование. Пусть заданной конечной клеткой является клетка 52. На последнем шаге в эту клетку можно попасть из клеток 41, 42,... 44. Запишем стоимости перехода из каждой из этих клеток в клетку 52 как характеристики клеток (на рис. 56 характеристики указаны в кружках), после чего перейдем к выбору решения на предпоследнем шаге. Из клетки 31 можно перейти в любую из клеток четвертого столбца, а из нее — в клетку 52, всего возможны четыре пути. Сравним их между собой и выберем путь с наименьшей стоимостью (с учетом стоимости движения из клетки четвертого столбца в конечную клетку 52). Стоимость перехода в клетку 52 по наилучшему пути запишем как характеристику клетки 31. Повторим эту процедуру для каждой из клеток третьего столбца. На рис. 9.15 выписаны характеристики всех клеток третьего столбца и для каждой клетки показан оптимальный путь. Переходя теперь ко второму столбцу, убеждаемся, что для каждой из клеток этого столбца нужно сравнить между собой только четыре варианта пути. Действительно, если, например, находясь в клетке 21, мы избрали путь в клетку 31, то над дальнейшим выбором пути задумываться уже не надо — оптимальный путь из клетки 31 был определен на предыдущем шаге исследования, а согласно принципу оптимальности, этот путь не зависит от того, каким образом мы попали в клетку 31. Заполнив характеристики клеток второго столбца, переходим к последнему шагу решения — складываем стоимости перехода из заданной клетки 13 с характеристиками клеток второго столбца и выбираем наименьшую из сумм. Пусть наименьшая сумма соответствует переходу в клетку 21. Тогда оптимальной траекторией (рис. 9.15) будет последовательность 13—21—31—41—52.

Подсчитаем теперь, сколько сравнений возможных путей необходимо провести при решении общей задачи выбора траектории на поле из m · n клеток. В каждом из столбцов, кроме крайних, необходимо сделать n ² сравнений путей (по n путей в каждой из n клеток), в крайних столбцах — по n сравнений, т. е. всего будет 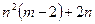сравнений, а это гораздо меньше, чем 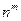путей при прямом переборе. Так, при n = m = 10 при прямом переборе надо сравнить 10 000 000 путей, а при использовании динамического программирования — 820. В сокращении числа кривых сравнения заключается основное достоинство алгоритмов, основанных на идеях динамического программирования.

Непрерывные задачи оптимального управления могут быть сведены к дискретным выборам достаточно малого шага квантования. Однако при уменьшении шага объем вычислений быстро возрастает, и численные алгоритмы динамического программирования требуют для своей реализации весьма быстродействующих вычислительных машин. Работа по совершенствованию алгоритмов вычисления оптимального управления продолжается.

Динамическое программирование особенно удобно при решении таких задач оптимизации, которые по своему существу дискретны, а также при большом количестве ограничений сложного вида. В то же время следует иметь в виду, что хотя принцип оптимальности, на котором основано динамическое программирование, является весьма общим (и, в частности, применим даже к некоторым неаддитивным функционалам), его нельзя использовать непосредственно для решения изопериметрических задач, поскольку условие, которому должна удовлетворять кривая, доставляющая экстремум (постоянство значения заданного функционала), относится в данном случае ко всей кривой, а не к ее части.