2015-03-22
581
Рассмотрим метод решения задач оптимального управления при отсутствии ограничений на фазовые координаты. Система (9.75) называется автономной, если в ее правую часть явно не входит время t.
Пусть в фазовом пространстве Х заданы две точки x 0 = (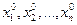
) и x 1 = (
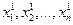). Если начальное и конечное положения изображающей точки в фазовом пространстве определены по всем n координатам, то задачу об оптимальном управлении называют задачей с закрепленными концами.
Рассмотрим следующую задачу. Требуется среди допустимых управлений u (t), t 0 ≤ t ≤ t 1, т.е. кусочно-непрерывных вектор-функций u (t)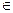 
U (моменты t 0 и t 1 не фиксированы), переводящих фазовую точку системы (9.75) из заданного начального положения x 0 (x( t 0 ) = x 0) в заданное конечное положение x 1 (x( t 1 ) = x 1), найти управление и траекторию при ограничениях вида (9.76) или (9.77), минимизируя при этом функционал
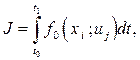i = 1: n, j = 1: m.
Управление u (t)итраектория х (t), решающие поставленную задачу, называются оптимальными.
Особое внимание уделяется частному случаю, когда f 0 = 1. В этом случае функционал
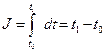
задает время движения. Управление и траектория, минимизирующие функционал, называются оптимальными по быстродействию.
Как показано выше (см. п. 9.6) уравнения Эйлера (9.10) представляют собой систему n уравнений второго порядка. Такую систему всегда можно свести к системе 2 n уравнений первого порядка. Наиболее удобны уравнения Эйлера в так называемой форме Гамильтона.
Введем новые переменные
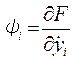(9.80)
и функцию
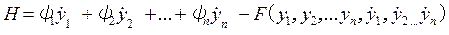, (9.81)
где ψ i – канонические переменные, H – функция Гамильтона.
Из выражения (9.81) следует, что
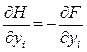, i = 1: n (9.82)
Уравнения Эйлера (9.10) перепишутся в виде
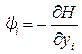, i = 1: n. (9.83)
Из выражения (9.81) также следует
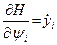, i = 1: n. (9.84)
Объединяя уравнения (9.83), (9.84) получаем так называемую Гамильтонову форму уравнений Эйлера (2 n уравнений Эйлера-Гамильтона)
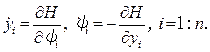(9.85)
