2015-03-22
1144
Пусть u (t) – управление, переводящее изображающую точку из положения x (t 0) в положение x (t 1), t 0 ≤ t ≤ t 1, а x (t) – соответствующая этому управлению траектория, переводящая фазовую точку х системы (9.75) из заданного начального положения х 0 в заданное конечное положение х 1,.где x (t 0) = х 0, x (t 1) = х 1.Если управление u (t) и х (t) – оптимальное управление и оптимальная траектория, то найдется такая непрерывная вектор-функция ψ (t), удовлетворяющая уравнениям
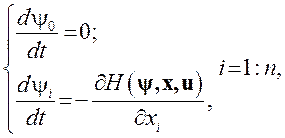(9.86)
что:
1) в каждый момент времени t, t 0 ≤ t ≤ t 1, функция H (ψ (t), x (t), u), рассматриваемая как функция переменного u, достигает в точке u = u (t) максимума
H [(ψ (t), x (t), u( t)] = М [(ψ (t), x (t)];
2) выполнено условие нетривиальности решения системы уравнений (9.86)
ψ( t ) ≠ 0;
3) в конечный момент времени t 1
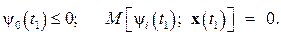
Для задачи о максимальном быстродействии, когда функционалом, минимум которого отыскивается, является время
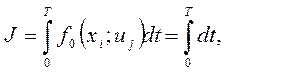(9.69)
уравнение для переменного ψ0 отпадает и функция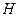 
принимает вид
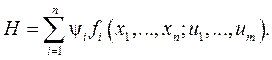
Оказывается, что при оптимальном управлении функции H (t) и ψ0(t) остаются постоянными и принимают значения:
H (t), a ψ0(t) ≤ 0. (9.70)
Сформулированное условие является лишь необходимым, а не достаточным. Принцип максимума устанавливает связь между управлением и координатами прямой и сопряженных систем. В связи с этим решение задачи сводится к выбору таких начальных значений сопряженной системы, при которых фазовая траектория управляемой системы будет переходить из начального xi (t 0) в требуемое конечное положение xi (t 1).
Заметим, что задачу о минимуме любого функционала (9.62) можно свести к задаче о быстродействии, введя новую переменную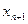 
и дополнительное уравнение
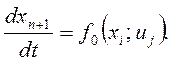
Пользуясь теоремой о максимуме, можно фактически определять оптимальные уравнения uj (t), доставляющие минимум функционалу (9.62) при учете уравнений связи (9.61). Действительно, для определения 2 n + k неизвестных функций x 1, x 2,…, xn, ψ1, ψ2,…, ψ n, u 1, u 2,…, uk имеем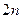 
уравнений (9.65) и (9.66) и k уравнений следуют из условия максимума гамильтониана H (9.64) по управлениям u 1, u 2,…, uk. Отметим, что, используя теорему о максимуме, мы отыскиваем решение не в классе кусочно-гладких функций, а в более обширном классе – классе кусочно-непрерывных функций.
Пример 9.6. Найти для объекта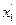 
= х 2, 
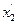= u управление, которое переводит объект из состояния х (0) = (1;1) в состояние покоя за 5 секунд, затратив минимум энергии. Функционал качества 
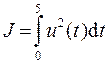, множество цели – точка х (5) = (0;0).
Решение. Составим функцию Гамильтона (9.81)
H (х, u, ψ) =- u 2 + ψ1 х 2 +ψ2 u.
Максимизируем функцию Гамильтона по управлению и найдем оптимальное управление:
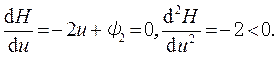
Получаем значение оптимального управления u * = 0,5 ψ2(t).
Каноническая система будет представлена уравнениями:
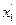= х 2; 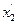= 0,5 ψ2(t);
х 1(0) = х 2(0) = 1; х 1(5) = х 2(5) = 0;
Используя (9.83), получаем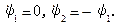 
Из канонической системы следует:
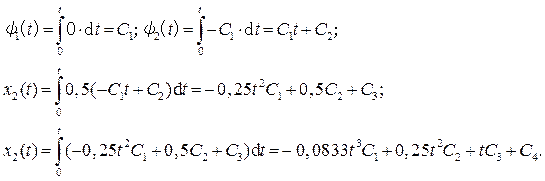
Постоянные интегрирования находим из краевых условий:
t = 0 С 3 = С 4 = 0; С 1 = -0,67; С 2 = -2,079.
Оптимальное управление u * = (0,67t – 2,08)/2.
.
