Рассмотрим коаксиальную кабельную линию длиной 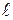 (рис.3.10) и определим ее параметры - активное сопротивление
(рис.3.10) и определим ее параметры - активное сопротивление 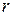 прямого и обратного провода, индуктивность
прямого и обратного провода, индуктивность 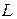 , емкость
, емкость 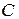 , а также проводимость утечки изоляции кабеля
, а также проводимость утечки изоляции кабеля 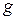 .
.

Пусть известны радиус жилы 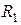 , внутренний и внешний радиусы оболочки
, внутренний и внешний радиусы оболочки 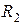 ,
, 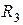 . Удельная электрическая проводимость материала жилы и оболочки
. Удельная электрическая проводимость материала жилы и оболочки 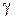 , магнитная проницаемость
, магнитная проницаемость 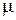 . Диэлектрическая проницаемость изоляции, расположенной между жилой и оболочкой равна
. Диэлектрическая проницаемость изоляции, расположенной между жилой и оболочкой равна 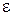 , удельная проводимость изоляции
, удельная проводимость изоляции 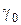 .
.
Сопротивление коаксиальной линии постоянному току складывается из сопротивлений внутреннего сплошного цилиндрического провода и внешнего трубчатого провода оболочки и равно
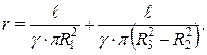
Индуктивность коаксиального кабеля равна 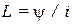 , где полное потокосцепление определится в виде
, где полное потокосцепление определится в виде
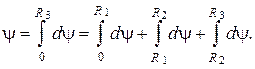
Первое слагаемое в этом выражении представляет собой потокосцепление, обусловленное внутренним магнитным потоком цилиндрического провода, и равно 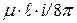 (см. раздел "Магнитное поле").
(см. раздел "Магнитное поле").
Поскольку магнитный поток в диэлектрике охватывает весь ток 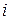 внутреннего провода, можем записать
внутреннего провода, можем записать
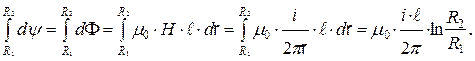
Это потокосцепление определяет так называемую внешнюю индуктивность кабеля на постоянном токе.
Замыкающийся в оболочке магнитный поток сцеплен не только с током 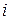 прямого провода, но и с частью тока, протекающего по оболочке
прямого провода, но и с частью тока, протекающего по оболочке 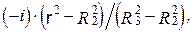 поэтому
поэтому
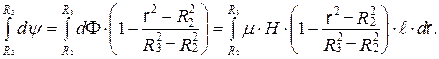
Из закона полного тока напряженность магнитного поля 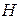 в оболочке определится из соотношения
в оболочке определится из соотношения
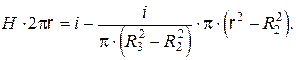
Следовательно,
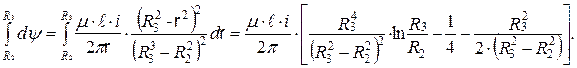
Подставив полученные аналитические выражения для интегралов в соотношение для потокосцепления коаксиального кабеля, получим формулу для расчета его индуктивности в виде
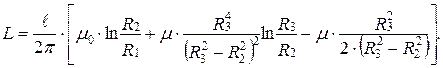
На практике обычно пренебрегают магнитным потоком в оболочке кабеля вследствие малости ее толщины, что значительно упрощает выражение для определения индуктивности:
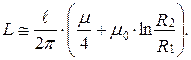
В пространстве между жилой и оболочкой кроме магнитного поля существует и электрическое поле. Поэтому кабель обладает емкостью 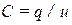 , где
, где 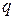 - заряд отрезка жилы кабеля длиной
- заряд отрезка жилы кабеля длиной 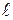 ,
, 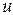 - разность потенциалов между внутренним и внешним проводниками.
- разность потенциалов между внутренним и внешним проводниками.
Разность потенциалов 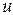 определим как линейный интеграл от напряженности электрического поля, взятый по радиальному направлению в пространстве между проводниками
определим как линейный интеграл от напряженности электрического поля, взятый по радиальному направлению в пространстве между проводниками 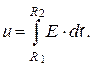
Выражение для функции 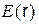 получим, используя постулат Максвелла
получим, используя постулат Максвелла 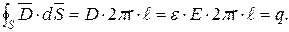 Следовательно,
Следовательно,
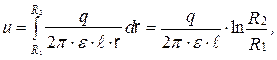
и для емкости коаксиального кабеля имеем:
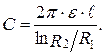
При несовершенстве изоляции между проводниками под действием электрического поля возникает ток утечки. Этот ток зависит от проводимости изоляции кабеля 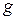 . Величина ее может быть найдена как отношение тока утечки в изоляции
. Величина ее может быть найдена как отношение тока утечки в изоляции 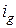 к разности потенциалов между проводниками
к разности потенциалов между проводниками 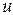 :
:
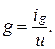
Ток утечки определится выражением 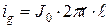 , где
, где 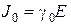 - плотность тока утечки в изоляции. Этот ток протекает через цилиндрическую поверхность площадью
- плотность тока утечки в изоляции. Этот ток протекает через цилиндрическую поверхность площадью 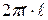 . Выразив разность потенциалов между проводниками через ток утечки
. Выразив разность потенциалов между проводниками через ток утечки
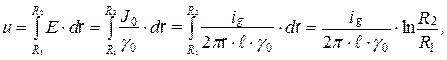
получим следующее выражение для расчета проводимости изоляции
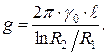
 2015-03-22
2015-03-22 8705
8705
