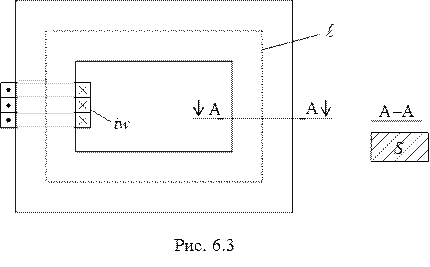
Определим магнитный поток 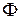 для сердечника с постоянным поперечным сечением
для сердечника с постоянным поперечным сечением 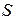 (рис. 6.3), считая м.д.с.
(рис. 6.3), считая м.д.с. 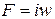 катушки известной.
катушки известной.
Учитывая допущение о равномерном распределении потока по сечению, из определения магнитного потока 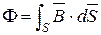 получим для рассматриваемой магнитной цепи
получим для рассматриваемой магнитной цепи
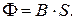
Применяя закон полного тока в интегральной форме к контуру 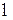 , являющемуся средней линией сердечника, можем записать
, являющемуся средней линией сердечника, можем записать
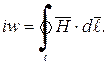
Используя допущение о неизменности потока вдоль контура 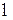 при постоянном сечении
при постоянном сечении 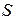 , получим
, получим
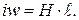
Соотношение 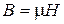 , с учетом полученных ранее выражений, приводит к равенству
, с учетом полученных ранее выражений, приводит к равенству
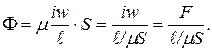
Отношение магнитодвижущей силы (м.д.с.) 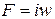 вдоль всей магнитной цепи к магнитному потоку
вдоль всей магнитной цепи к магнитному потоку 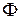 называют магнитным сопротивлением такой цепи
называют магнитным сопротивлением такой цепи
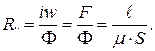
Размерность магнитного сопротивления [ 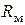 ] = 1/Гн.
] = 1/Гн.
Понятие магнитного сопротивления можно ввести и для участка магнитной цепи. В этом случае 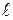 представляет собой длину участка магнитопровода с сечением
представляет собой длину участка магнитопровода с сечением 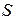 . Магнитное сопротивление является основным параметром магнитной цепи.
. Магнитное сопротивление является основным параметром магнитной цепи.
Соотношение
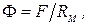
связывающее магнитный поток, м.д.с. и магнитное сопротивление сердечника, называют законом Ома для магнитной цепи.
Полученное выражение аналогично закону Ома для электрической цепи
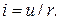
Сравнивая интегральные характеристики магнитных и электрических цепей, можно установить аналогию между ними.
Таблица 6.1
| Магнитная цепь | Электрическая цепь |
Магнитный поток 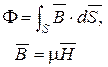 М.д.с. М.д.с. 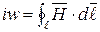 М.д.с. на участке АВ М.д.с. на участке АВ 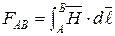 Магнитное сопротивление Магнитное сопротивление 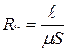 Закон Ома для участка магнитной цепи Закон Ома для участка магнитной цепи 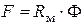 Схема магнитной цепи Схема магнитной цепи 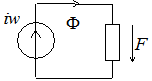 | Электрический ток 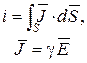 Э.д.с. Э.д.с. 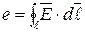 Напряжение на участке АВ Напряжение на участке АВ 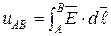 Электрическое сопротивление Электрическое сопротивление 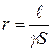 Закон Ома для участка электрической цепи Закон Ома для участка электрической цепи 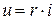 Схема электрической цепи Схема электрической цепи  |
 2015-03-22
2015-03-22 2084
2084
