2015-03-22
5129
Изложение метода узловых напряжений начнем с рассмотрения направленного графа схемы (рис.5.10), токи в ветвях которой необходимо определить.
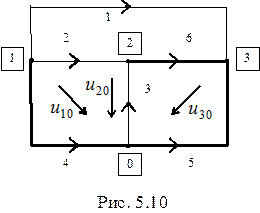Дерево графа выделено на рисунке утолщенными линиями. Предположим, что известны напряжения на ветвях цепи, соответствующих у графа ветвям дерева (ветви 4,5,6). В этом случае напряжения на остальных ветвях могут быть определены из уравнений, составленных по второму закону Кирхгофа для независимых контуров цепи (т.е. образованных одной связью и ветвями дерева):
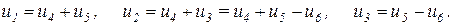
Это свойство напряжений ветвей дерева сохраняется при любом выборе дерева графа. Таким образом, по известным напряжениям на ветвях цепи, соответствующих в графе ветвям дерева, напряжения остальных ветвей могут быть определены исходя из второго закона Кирхгофа без решения системы уравнений.
Введем в рассмотрение так называемые узловые напряжени я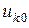 
, понимая под ними напряжения между 
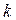-ым узлом и нулевым (опорным) узлом. В общем случае опорный узел выбирается произвольно. Для принятой на рис. 5.10 нумерации узлов получаем узловые напряжения 
, 
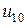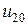и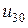 
. Иная нумерация узлов породит иные узловые напряжения. При этом их общее число (три в данном примере) остается неизменным и будет равно для произвольной цепи 
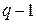, где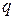 
- число узлов цепи.
Важным обстоятельством в данной ситуации является то, что напряжение на любой из ветвей цепи может быть выражено через узловые напряжения. В рассматриваемом примере для ветвей дерева
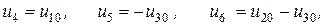
и, следовательно, для связей
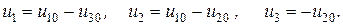
В общем случае, для ветви, находящейся между узлам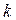и и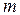 
, можно записать 
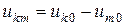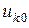, где и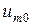 
- узловые напряжения соответственно между узлами 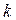, 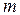и опорным узлом. Таким образом, расчет узловых напряжений фактически определяет напряжения на всех ветвях цепи, а значит и токи в них.
Система уравнений для определения узловых напряжений в произвольной цепи имеет вид
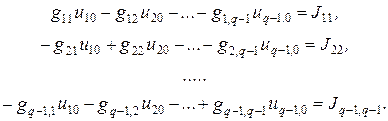
Для уяснения правил формирования коэффициентов системы уравнений и их правых частей рассмотрим следующий пример. Определим токи в ветвях схемы, изображенной на рис. 5. 11.
Выбрав опорный узел 0 и пронумеровав остальные узлы, запишем для них уравнения по первому закону Кирхгофа
(*)
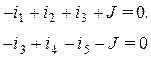Для данной системы (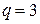
) имеем два узловых напряжения 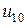и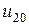 
. Выразим токи ветвей через узловые напряжения
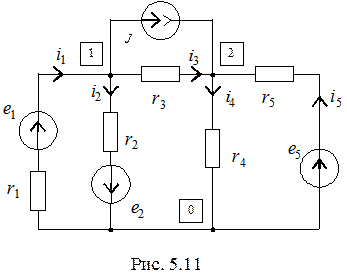
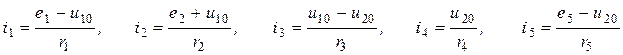
и подставим полученные выражения в уравнения (*). Группируя подобные слагаемые, получаем
(**)
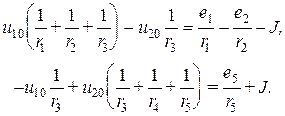Система уравнений (**) примет характерный для метода узловых напряжений вид
(***)
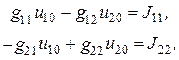если обозначить
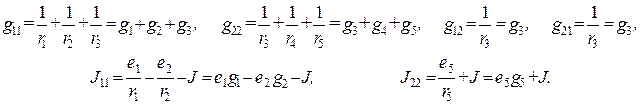
Полученные выражения позволяют сформулировать правила формирования коэффициентов системы уравнений и их правых частей:
· диагональные элементы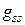 
матрицы коэффициентов представляют собой сумму проводимостей ветвей, подходящих к 
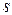-му узлу;
· недиагональные элементы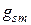 
представляют собой проводимость ветви (или суммарную проводимость ветвей), соединяющей узлы 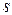и 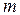, при этом 
;
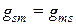· правые части уравнений, так называемые задающие токи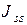 
, рассчитываются как алгебраическая сумма источников тока, подходящих к 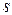-му узлу, причем знак (+) приписывают слагаемым, если источник направлен к узлу, а знак (-) - в противном случае.
Входящие в выражения для задающих токов слагаемые вида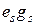 
имеют смысл эквивалентных источников тока, соответствующих неидеальным источникам э.д.с.
Решение системы (***) может быть записано в виде
где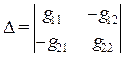 
главный определитель системы уравнений,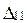 
, 
, 
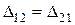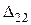- алгебраические дополнения.
Рассчитав узловые напряжения, нетрудно определить ток в любой ветви схемы
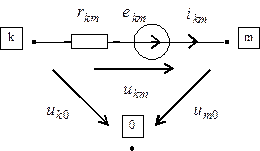
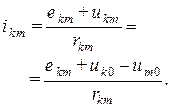
Отметим особенности использования метода узловых напряжений при расчете схем с идеальными источниками э.д.с.
При наличии в цепи идеального источника э.д.с. е в качестве опорного узла необходимо выбрать один из узлов ветви, включающей в себя этот источник. Такой выбор означает, что узловое напряжение этой ветви равно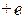 
или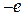 
в зависимости от направления э.д.с. по отношению к опорному узлу. Порядок системы уравнений (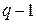) МУН уменьшается на единицу, так как исключается уравнение, в правой части которого содержится задающий ток для узла ветви с идеальным источником э.д.с.
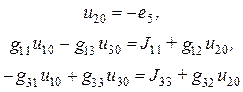
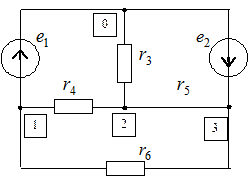При наличии в схеме нескольких ветвей с идеальными источниками э.д.с., имеющих общий узел, в качестве опорного узла выбирается именно этот узел.
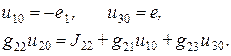
Если конфигурация схемы отличается от описанных вариантов, то, используя перенос идеального источника э.д.с. через узел, следует привести схему к требуемому виду
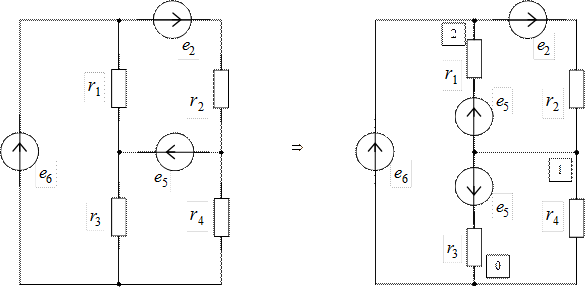
Система уравнений для определения узловых напряжений 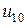, 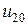в преобразованной цепи может быть записана следующим образом:
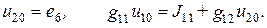
Рассмотрим формирование уравнений по методу узловых напряжений при наличии зависимых источников. Вначале зависимые источники в системе уравнений учитываются в правой части системы как независимые. Затем, используя уравнения Кирхгофа, управляющие токи и напряжения выражаются через узловые напряжения. В завершающем этапе содержащие узловые напряжения слагаемые из правой части системы уравнений переносятся влево от знака равенства и группируются с соответствующими элементами системы.
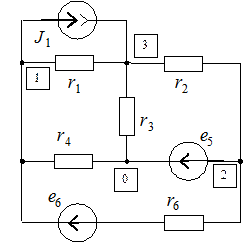
В качестве примера сформируем систему уравнений по методу узловых напряжений для изображенной на рисунке схемы.
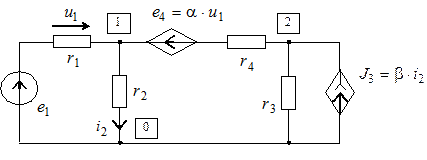
Для данной схемы 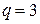. Система уравнений, составленная по методу узловых напряжений, имеет порядок 
:
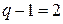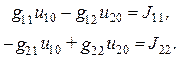
Определим значения коэффициентов
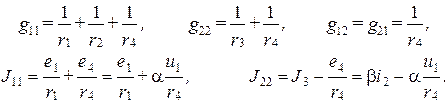
Выразим управляющие переменные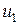 
и 
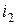через узловые напряжения. Можно записать: 
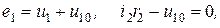тогда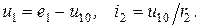 
Подставим полученные соотношения в выражения для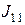 
, 
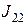
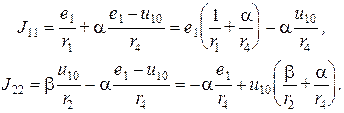
Окончательно получим следующую систему уравнений
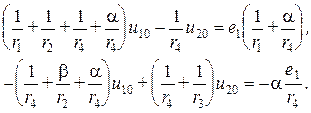
Сопоставляя методы контурных токов и узловых напряжений, можно рекомендовать метод контурных токов в тех случаях, когда число независимых контуров графа цепи меньше числа узлов без единицы и метод узловых напряжений при выполнении обратного неравенства.
