Расчет для постоянной составляющей.
Входное напряжение 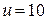 В.
В.
Конденсатор постоянный ток не проводит, поэтому 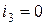 . Напряжения на зажимах катушек индуктивности равны нулю при протекании постоянного тока, следовательно
. Напряжения на зажимах катушек индуктивности равны нулю при протекании постоянного тока, следовательно 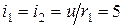 А.
А.
Расчет для первой гармоники.
Входное напряжение 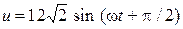 .
.
Воспользуемся комплексным методом расчета. Комплексное напряжение на входе цепи имеет вид 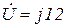 В. Запишем комплексные сопротивления ветвей:
В. Запишем комплексные сопротивления ветвей:
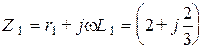 Ом,
Ом, 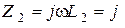 Ом,
Ом, 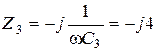 Ом.
Ом.
Эквивалентное комплексное сопротивление цепи получим из соотношения
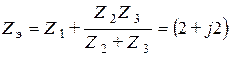 Ом.
Ом.
Далее имеем
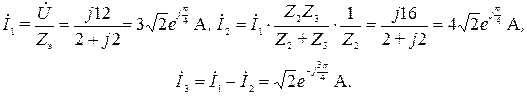 Мгновенные значения токов в ветвях для первой гармоники определяются выражениями:
Мгновенные значения токов в ветвях для первой гармоники определяются выражениями:
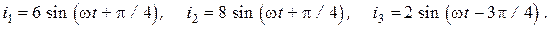
Расчет для второй гармоники.
Входное напряжение 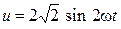 .
.
Комплексное напряжение на входе цепи равно 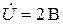 . Комплексные сопротивления ветвей синусоидальному току частотой
. Комплексные сопротивления ветвей синусоидальному току частотой 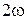 равны
равны
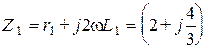 Ом,
Ом, 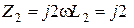 Ом,
Ом, 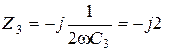 Ом.
Ом.
Эквивалентное сопротивление участка 2,3 цепи равно
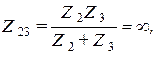
то есть на участке цепи, образованном двумя параллельно соединенными ветвями 2 и 3, имеет место резонанс токов и 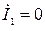 .
.
Ток во второй ветви найдем из уравнения, составленного согласно второму закону Кирхгофа
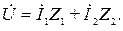
В результате имеем 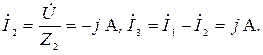 Мгновенные значения токов второй гармоники определяются выражениями
Мгновенные значения токов второй гармоники определяются выражениями
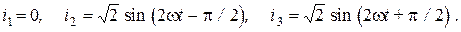
Окончательно мгновенные значения токов в ветвях цепи найдем, суммируя их значения для отдельных гармоник:
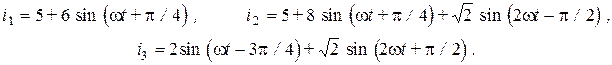
Обратим внимание на следующее обстоятельство. Соотношение амплитудных значений первой и второй гармоник напряжения 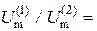 6. В то же время соотношение амплитудных значений гармоник тока, например в третьей ветви,
6. В то же время соотношение амплитудных значений гармоник тока, например в третьей ветви, 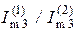
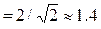 , а для тока первой ветви
, а для тока первой ветви 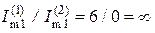 , что связано с изменением сопротивлений реактивных элементов на различных частотах. Таким образом, изменяя структуру схемы и подбирая параметры реактивных элементов, можно изменять гармонический состав токов при произвольном несинусоидальном воздействии.
, что связано с изменением сопротивлений реактивных элементов на различных частотах. Таким образом, изменяя структуру схемы и подбирая параметры реактивных элементов, можно изменять гармонический состав токов при произвольном несинусоидальном воздействии.
Найдем действующие значения токов ветвей и входного напряжения
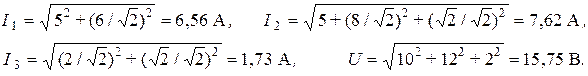
Активная мощность потребляется в ветвях с резисторами и в данной цепи 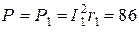 Вт. Активная мощность, отдаваемая источником, равна
Вт. Активная мощность, отдаваемая источником, равна
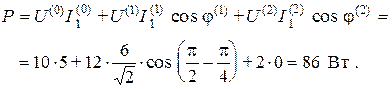
В последнем выражении индекс в скобках указывает номер гармоники, для которой определены действующие значения входного напряжения 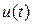 и тока
и тока 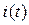 .
.
Равенство активных мощностей приемника и источника соответствует условию баланса мощности и подтверждает правильность расчета.
Задача 2. Рассчитать и построить амплитудно-частотные характеристики тока 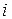 , напряжения на конденсаторе
, напряжения на конденсаторе 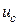 , напряжения на катушке индуктивности
, напряжения на катушке индуктивности 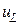 для двухполюсников, изображенных на рисунке. К зажимам цепи приложено напряжение
для двухполюсников, изображенных на рисунке. К зажимам цепи приложено напряжение 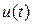 , для которого разложение в ряд Фурье имеет вид:
, для которого разложение в ряд Фурье имеет вид:
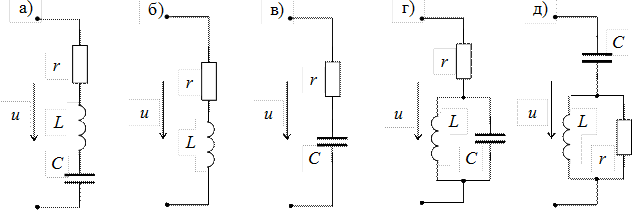 Параметры элементов двухполюсников:
Параметры элементов двухполюсников: 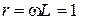 Ом,
Ом, 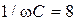 Ом.
Ом.
Рассмотрим решение задачи для первого варианта схемы.
Амплитуду 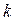 -ой гармоники тока
-ой гармоники тока 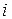 определим из соотношения
определим из соотношения
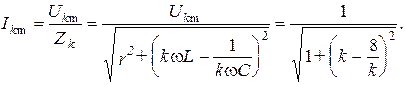
Тогда амплитуды 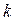 -ой гармоники напряжения на конденсаторе
-ой гармоники напряжения на конденсаторе 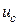 и напряжения на катушке индуктивности
и напряжения на катушке индуктивности 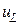 могут быть рассчитаны следующим образом
могут быть рассчитаны следующим образом
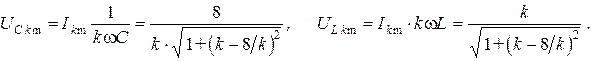
Результаты расчета дискретных спектров 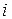 ,
, 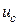 ,
, 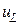 приведены в таблице 12.1, а соответствующие амплитудно-частотные характеристики изображены на рисунке.
приведены в таблице 12.1, а соответствующие амплитудно-частотные характеристики изображены на рисунке.
Таблица 12.1
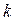 |  | |||||
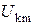 | ||||||
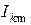 | 0,141 | 0,447 | 0,832 | 0,447 | 0,282 | |
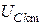 | 1,128 | 1,790 | 2,220 | 0,894 | 0,451 | |
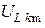 | 0,141 | 0,894 | 2,500 | 1,780 | 1,410 |
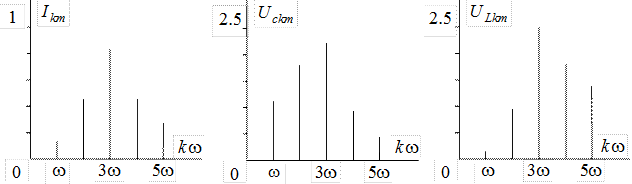
Обратим внимание на максимумы в дискретных спектрах при 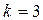 . Частота
. Частота 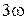 не является резонансной для рассматриваемого колебательного контура, однако близка к ней, чем и определяется наличие экстремумов.
не является резонансной для рассматриваемого колебательного контура, однако близка к ней, чем и определяется наличие экстремумов.
Задача 3. Напряжение на входе фильтра имеет вид
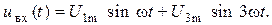
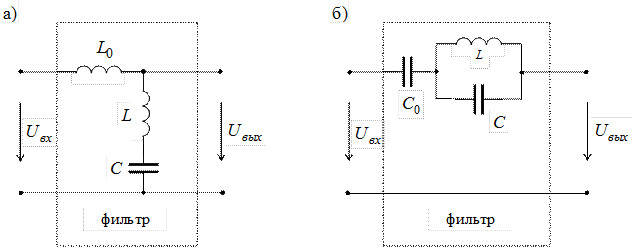
Определить параметры элементов фильтра таким образом, чтобы в кривой напряжения 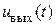 на зажимах приемника отсутствовала третья гармоника, а первая гармоника передавалась без искажения от источника к приемнику.
на зажимах приемника отсутствовала третья гармоника, а первая гармоника передавалась без искажения от источника к приемнику.
Вариант а. Отсутствие третьей гармоники в кривой 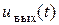 возможно в случае, когда сопротивление ветви
возможно в случае, когда сопротивление ветви 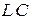 току третьей гармоники равно нулю. Это условие соответствует резонансу напряжений на частоте третьей гармоники в ветви
току третьей гармоники равно нулю. Это условие соответствует резонансу напряжений на частоте третьей гармоники в ветви 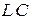 , что приводит к равенству
, что приводит к равенству
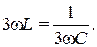
Передача без искажения основной гармоники напряжения от источника к приемнику означает равенство единице коэффициента передачи напряжения 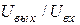 на частоте первой гармоники. Напряжение на выходе фильтра запишется в виде
на частоте первой гармоники. Напряжение на выходе фильтра запишется в виде
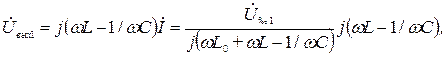
и, с учетом равенства 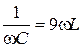 , получим
, получим
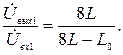
Далее имеем
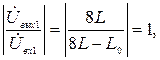
что соответствует двум равенствам: 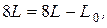 откуда
откуда 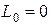 , и
, и 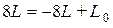 , откуда
, откуда 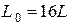 .
.
При условии 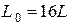 получаем
получаем 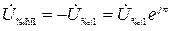 .
.
Решение, при котором 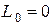 , также обеспечивающее равенство
, также обеспечивающее равенство 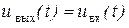 , одновременно приводит к замыканию накоротко источника на частоте третьей гармоники и поэтому должно быть отброшено.
, одновременно приводит к замыканию накоротко источника на частоте третьей гармоники и поэтому должно быть отброшено.
Задача имеет несколько решений, поскольку три неизвестных параметра определяются из двух условий.
Итак, при выполнении условий
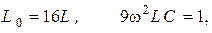
напряжение на выходе фильтра равно 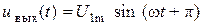 .
.
Вариант б. При подборе параметров 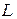 и
и 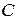 таким образом, чтобы выполнялось условие
таким образом, чтобы выполнялось условие 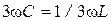 , соответствующее резонансу токов на частоте третьей гармоники, сопротивление двухполюсника
, соответствующее резонансу токов на частоте третьей гармоники, сопротивление двухполюсника 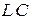 в фильтре будет бесконечно большим. Тогда третья гармоника тока на выходе фильтра и, следовательно, третья гармоника напряжения
в фильтре будет бесконечно большим. Тогда третья гармоника тока на выходе фильтра и, следовательно, третья гармоника напряжения 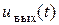 , будет отсутствовать.
, будет отсутствовать.
Емкость 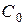 следует подобрать таким образом, чтобы сопротивление фильтра току первой гармоники равнялось нулю. В результате, с учетом условия
следует подобрать таким образом, чтобы сопротивление фильтра току первой гармоники равнялось нулю. В результате, с учетом условия 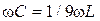 , получим
, получим
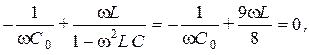
откуда 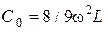 .
.
Окончательно имеем следующие два соотношения для определения трех параметров фильтра
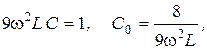
при этом 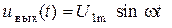 .
.
Задача выбора параметров 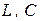 и
и 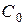 , как и предыдущая, имеет несколько решений.
, как и предыдущая, имеет несколько решений.
 2015-03-22
2015-03-22 2164
2164
