Основные определения и классификация

ОБЩИЕ СВОЙСТВА ЧЕТЫРЕХПОЛЮСНИКОВ

Электротехнические устройства, служащие для передачи энергии или сигналов, имеющие два входных и два выходных зажима, называются четырехполюсниками. Различают активные и пассивные четырехполюсники. Вактивных четырехполюсниках внутри содержатся источники электрической энергии, пассивные четырехполюсники источников энергии не содержат. Зажимы четырехполюсника, к которым присоединяется источник электрической энергии, называют входными, зажимы, к которым присоединяют нагрузку - выходными. В качестве пассивных четырехполюсников могут рассматриваться трансформаторы, электрические фильтры и т.д.

1-1' - входные зажимы 2-2' - выходные зажимы

В настоящем разделе будем рассматривать только пассивные четырехполюсники при установившихся синусоидальных процессах. Активные четырехполюсники могут быть заменены пассивными с вынесенными за входные и выходные зажимы эквивалентными источниками э.д.с. и тока.

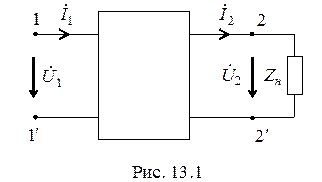Для анализа работы четырехполюсника выберем направления токов и напряжений 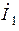, , 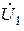, , 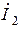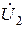соответствующие перетоку электрической энергии от входных к выходным зажимам, что совпадает с принятым определением четырехполюсника (рис. 13.1).

Рассмотрим соотношения между входными и выходными напряжениями и токами четырехполюсника.

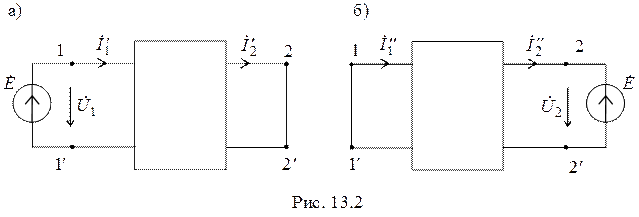В режиме короткого замыкания со стороны выходных зажимов (рис. 13.2 а) для четырехполюсника, составленного из линейных элементов, токи 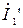на входе и 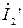на выходе пропорциональны входному напряжению :

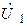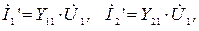
где 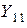- входная и 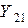- переходная проводимости четырехполюсника.

Аналогично, при коротком замыкании со стороны входных зажимов (рис. 13.2 б) имеем:

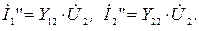
В соответствии с принципом наложения запишем уравнения четырехполюсника для произвольного режима:

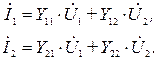(1)

Система уравнений (1) называется системой уравнений четырехполюсника, представленной в Y -параметрах.

Из четырех входящих в эти уравнения коэффициентов независимыми являются три параметра, поскольку для любого пассивного четырехполюсника справедливо свойство .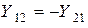

Запись уравнений четырехполюсника в Y -параметрах не является единственно возможной формой записи уравнений четырехполюсника. Из четырех величин 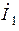, , 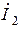, 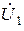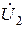в явном виде могут быть выражены любые две: 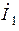, 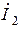; 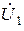, 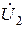; 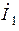, , 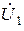и так далее. Таким образом, общее число различных по форме, но эквивалентных по существу систем уравнений, описывающих четырехполюсники, равно шести.

Три формы записи уравнений четырехполюсника носят общепринятые названия: уравнения четырехполюсника в 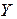-параметрах, приведенные выше, и уравнения в Z - и 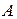-параметрах, которые будут рассмотрены далее.

Выражая входные и выходные напряжения через входные и выходные токи, получим систему уравнений четырехполюсника в Z - параметрах:

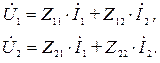(2)

Тот факт, что пассивный четырехполюсник характеризуется тремя независимыми параметрами, выражается равенством 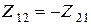. Часто используется также система уравнений четырехполюсника в 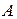-параметрах:

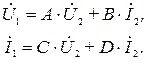(3)

В этом случае для коэффициентов системы уравнений справедливо выражение .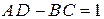

В матричной форме система (3) имеет вид:

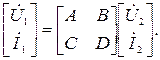
Отметим, что при любой форме записи уравнений пассивного четырехполюсника независимыми будут являться только три параметра.

Представленные системы уравнений характеризуют один и тот же четырехполюсник, поэтому и коэффициенты в этих уравнениях связаны между собой.

Таблица 14.1

	Z	Y	A
Z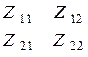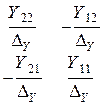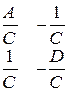
Y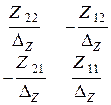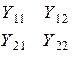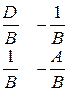
A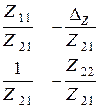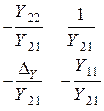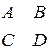

Для уяснения этих связей рассмотрим четырехполюсник вида

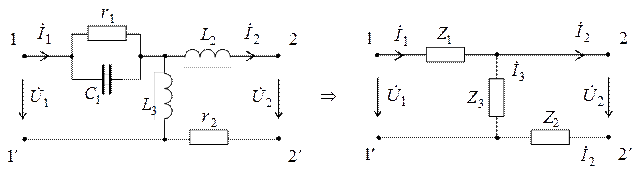Запишем выражения для комплексных сопротивлений ветвей

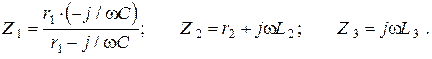
Сформировав систему уравнений Кирхгофа

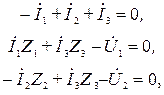
приведем ее к системе уравнений четырехполюсника в 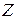-параметрах. Для этого исключим в исходных уравнениях переменную 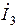. В результате получим систему уравнений вида:

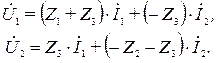(4)

Сопоставляя коэффициенты при токах системы уравнений четырехполюсника в 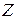-параметрах и последней системы, получим выражения для 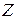- параметров рассматриваемого четырехполюсника:

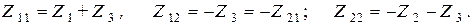(5)

Для определения 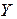-параметров данного четырехполюсника выразим в системе (4) ток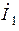и и 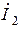через входное 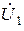и выходное 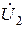напряжения с учетом соотношений (5)

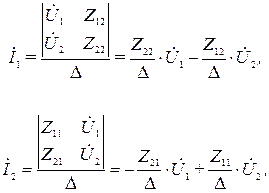
где 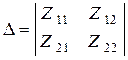- главный определитель системы (4).

Сопоставляя коэффициенты при напряжениях 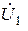и 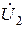полученной системы уравнений и системы уравнений (1), определим выражения для 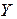-параметров рассматриваемого четырехполюсника:

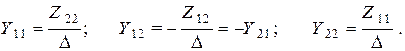(6)

В соотношениях (5), (6) проявляется справедливая для всех пассивных четырехполюсников закономерность

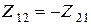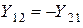и . (7)

Для определения 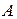-параметров рассматриваемого четырехполюсника преобразуем уравнения в 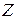-параметрах к виду (3)

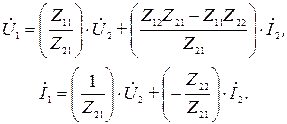
Сопоставляя коэффициенты полученной системы уравнений с коэффициентами 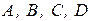системы уравнений (3), запишем:

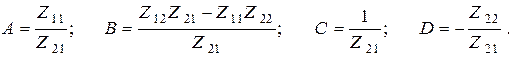
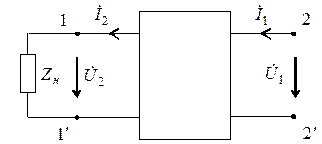Учитывая, что 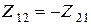, можно убедиться в справедливости соотношения 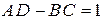непосредственной проверкой.

Поменяв местами входные и выходные зажимы изображенного на рис. 13.1 четырехполюсника, получим схему вида:

Сформируем для данного четырехполюсника систему уравнений в 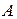-параметрах. Для этого выполним соответствующую замену переменных в уравнениях (3) четырехполюсника (рис. 13.1):

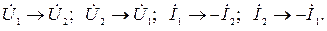
При этом указанная система уравнений преобразуется к виду:

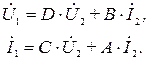
Таким образом, при замене входных зажимов четырехполюсника на выходные коэффициенты 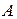и 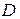в системе уравнений (3) меняются местами.

В случае, когда соотношения между токами и напряжениями не изменяются при замене входных зажимов четырехполюсника выходными, четырехполюсник является симметричным. Для симметричного четырехполюсника справедливы равенства:

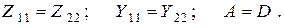
Целесообразность введения понятия "четырехполюсник" определяется тем, что оно позволяет сводить рассмотрение процессов передачи энергии или сигналов в сложных пассивных электрических цепях к анализу системы двух уравнений с тремя независимыми параметрами. Это обстоятельство определяет широкое использование теории четырехполюсников в электротехнических расчетах.