Действующие периодические несинусоидальные

Токи, напряжения, э.д.с.

Основываясь на определении действующего значения тока как его среднего квадратичного значения за период

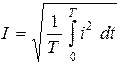
и раскладывая 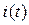в ряд Фурье, имеем

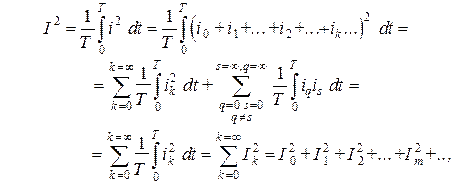
так как при 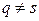получаем интегралы от синусоидальных функций за целое число (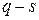) и (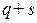) периодов. Такие интегралы равны нулю:

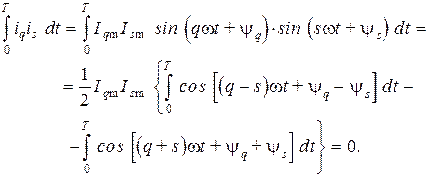
Окончательно имеем

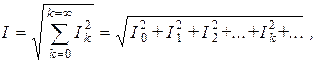
то есть действующее значение периодического несинусоидального тока равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений всех гармоник.

Аналогично находим выражения для периодических несинусоидальных напряжений и э.д.с.

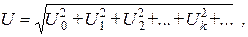
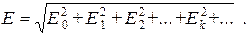
Активная мощность и коэффициент мощности