Каскадное соединение четырехполюсников

Представим уравнения четырехполюсника, записанные через 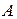-параметры, в матричной форме:

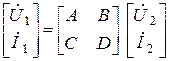или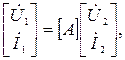

где 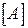- матрица -параметров четырехполюсника.

Рассмотрим так называемое каскадное соединение четырехполюсников

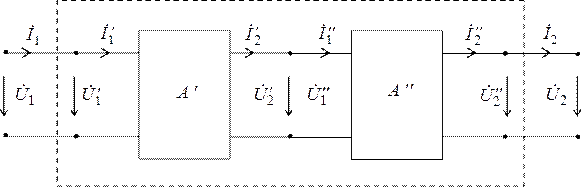
Для данного способа соединения справедливы соотношения:

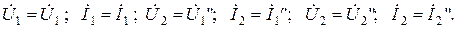
Задача заключается в определении параметров эквивалентного четырехполюсника через известные параметры первого и 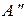второго четырехполюсников.

Для каждого из исходных четырехполюсников справедливы матричные равенства

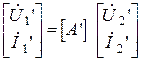и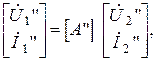

Используя эти соотношения, получим систему уравнений эквивалентного четырехполюсника в виде:

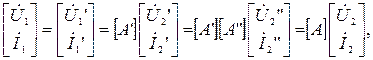
где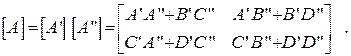

Таким образом, при каскадном соединении четырехполюсников матрица 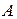-параметров составного четырехполюсника равна произведению матриц 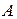-параметров отдельных четырехполюсников. Так как произведение матриц в общем случае не обладает свойством коммутативности 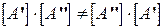, то и 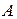- параметры составного четырехполюсника в общем случае зависят от последовательности включения отдельных четырехполюсников.